题目描述

给定一张 $n$ 个结点 $m$ 条边的带权图（可能为无向图，可能为有向图）。

定义其一个生成树 $T$ 的权值为 $T$ 中所有边权的乘积。

求其所有不同生成树的权值之和，对 $10^9+7$ 取模。

注意：

1. 本题中，有向图的生成树指的是 以 $1$ 为根的外向树；

2. 两棵生成树 $T_1,T_2$ 不同，当且仅当存在存在一条边 $e$，满足 $e\in T_1,\ \ e\notin T_2$。

输入格式

第一行：三个整数 $n,m,t$，分别表示图的结点数量，边的数量和图的类型（$t=0$ 时为无向图，$t=1$ 时为有向图）。

接下来 $m$ 行：每行三个整数 $u,v,w$。

如果 $t=0$，表示 $u,v$ 之间有一条权值为 $w$ 的无向边；

如果 $t=1$，表示从 $u$ 到 $v$ 有一条权值为 $w$ 的有向边。

输出格式

第一行：一个整数 $ans$，表示给定的图的生成树权值和对 $10^9+7$ 取模的结果。

5 8 0
2 3 1
1 2 3
4 5 1
4 2 2
3 5 2
3 4 3
3 4 1
3 3 5

144

5 9 1
1 2 3
3 2 1
1 3 1
2 4 2
3 5 1
4 3 4
3 5 1
5 4 1
4 4 6

72

提示

【样例 $1$ 解释】

样例 $1$ 中的无向图如左图所示：

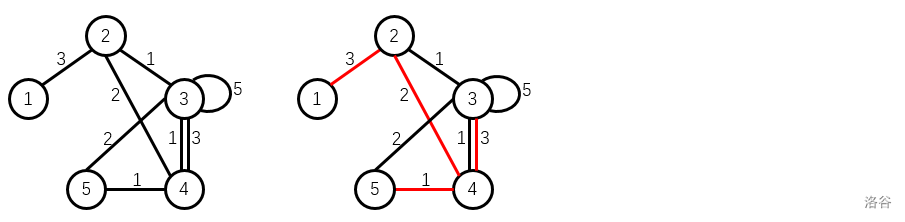
右图为其一个权值为 $3\times 1\times 2\times 3=18$ 的生成树的例子。

【样例 $2$ 解释】

样例 $2$ 中的有向图如左图所示：

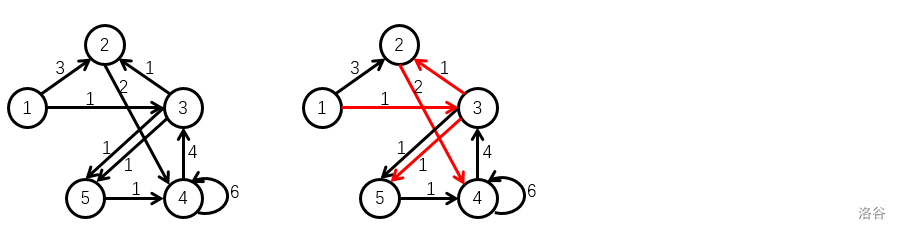
右图为其一个权值为 $1\times 1\times 1\times 2=2$ 的生成树（以 $1$ 为根的外向树）的例子。

【数据范围】

对于 $100\%$ 的数据：$1\leq n\leq 300,\ \ 1\leq m\leq 10^5,\ \ t\in \{0,1\},\ \ 1\leq u,v\leq n,\ \ 1\leq w\leq 10^9$。

对于测试点 $1,2,3,4,5,6$，$t=0$；对于测试点 $7,8,9,10,11$，$t=1$。

图中 可能 存在重边和自环，重边算作多条边。