题目描述

在李奥纳多的文献 "Codex Atlanticus" 中描述了一种早期而复杂的降落伞。李奥纳多的降落伞是一个由布料缝制而成的金字塔型木头结构。

串接的圆环

空中自由落体玩家 Adrain Nicholas （爱准尼古拉斯） 在五百年后测试了李奥纳多的设计。在这个测试中，一个现代的轻量结构将李奥纳多的降落伞使用到人体。我们想要使用串接的圆环，这些圆环为缝制的布料提供了钩子。圆环可以很简单地串接在一起，而且每一个圆环可以打开或关闭。串接的圆环可以构成一种特殊的型态叫做"链"（chain）。所谓的"链"指的是一序列串接的圆环，每个圆环可以串接（最多两个）邻居。但是这个序列必须有个起头与结束（这两个圆环只能串接另外一个圆环）。如下图所示。

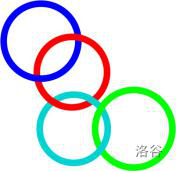
其他种串接型态当然是可能的，因为一个圆环可以串接到3个或更多的圆环。我们说一个圆环是"关键的"如果我们将它打开并移除这个圆环，其他的圆环会形成互无交集的链的集合(或者是没有任何的圆环留下)。

例子

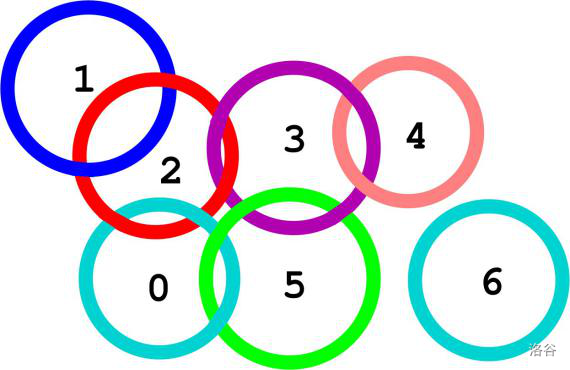
请参考下图中的 $7$ 个圆环，其编号由 $0$ 到 $6$。在这个例子中有两个"关键"圆环。其中一个关键圆环是编号 $2$ 的圆环。移除此圆环，剩下的圆环形成三条链 $[1]$, $[0,5,3,4]$ 以及 $[6]$。另外一个关键圆环是编号 $3$ 的圆环，移除此圆环，剩下的圆环形成三条链 $[1,2,0,5]$,$[4]$，以及 $[6]$。如果我们尝试着移除其他的圆环，我们无法获得互无交集的链集合。举例来说，移除编号 $5$ 的圆环之后，虽然可以获得 $[6]$ 这样的一条链，但是 $0,1,2,3$ 以及 $4$ 并没有形成一条链。

任务

给定一个串接的圆环型态，你的程序必须计算其关键圆环的个数。

输入格式

• 第一行，有 $2$ 个整数 $N$，$L$。$N$ 代表有 $N$ 个互无交集的圆环，其编号从 $0$ 到 $N-1$ 作为初始的圆环形态，$L$ 表示操作的个数。

• 第 $2$ 到 $L+1$ 行，每行包含 $1$ 或 $2$ 个整数，表示一个操作。具体如下：

1.A B 表示将编号 $A$ 以及编号 $B$ 的圆环串联在一起。保证 $A$ 和 $B$ 不相同。

2.-1 输出一行，目前串接圆环的组态中关键圆环的个数。

输出格式

对于每项 $2$ 操作，输出一行，表示当时串接圆环的组态中关键圆环的个数。

100 84
30 79
26 63
96 30
17 97
33 63
73 25
17 7
96 48
80 6
3 34
51 48
33 37
89 7
72 65
51 54
49 37
45 72
50 39
95 89
3 55
25 0
2 54
10 91
59 2
29 46
0 40
95 68
69 45
87 68
49 38
20 69
87 15
35 39
59 47
38 62
91 19
35 70
83 19
28 20
70 24
36 55
75 36
28 12
53 29
12 16
75 84
40 85
27 53
58 62
88 84
44 27
76 24
58 22
8 44
94 15
14 94
5 83
31 85
90 5
88 42
81 47
76 67
82 80
31 93
14 74
42 98
99 82
71 8
98 92
18 22
81 52
99 23
41 67
74 1
93 56
4 52
1 86
92 60
56 66
18 61
16 57
43 23
4 64
-1

100

提示

对于 $100\%$ 的数据，$1 \le N,L \le 10^6$。