Description

以氷屋为原点，三月精的位置分别记作向量 $\vec{a}$, $\vec{b}$, $\vec{c}$。

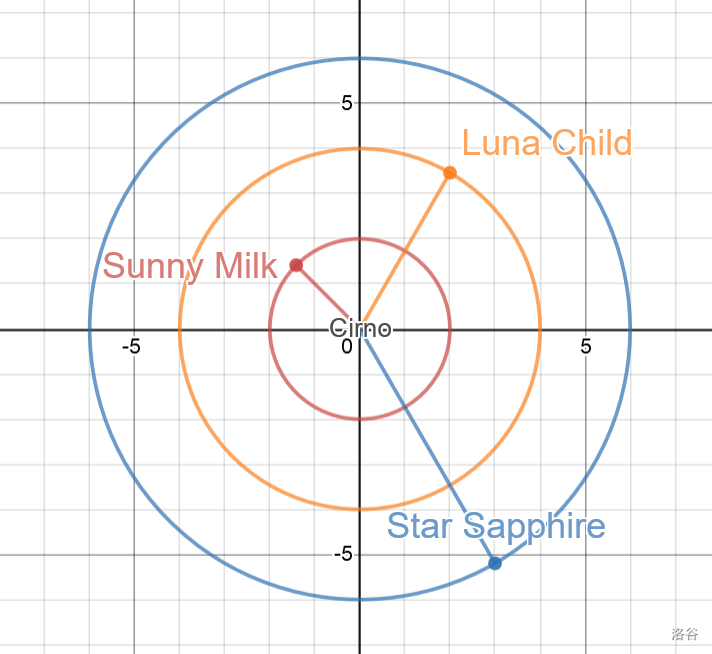
由定义可知，$|\vec{a}|=r_1$, $|\vec{b}|=r_2$, $|\vec{c}|=r_3$。

现在 Cirno 分配给你的任务是计算其 破坏极限指数 $\sigma$。

$$\sigma=\min\{\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{c}\cdot\vec{a}\}$$

其中「$\cdot$」表示 向量内积。

Input Format

一行，三个整数 $r_1$, $r_2$, $r_3$，保证 $r_1 \le r_2 \le r_3$。

Output Format

一行，一个 实数 $\sigma$。（小数点后保留一位数字）

3 4 5

-25.0

159 473 824 

-445561.0

Hint

Sample1 解释

$\cos\langle\vec{a},\vec{b}\rangle=0,\cos\langle\vec{b},\vec{c}\rangle=-\frac{4}{5},\cos\langle\vec{c},\vec{a}\rangle=-\frac{3}{5}$ 时答案最小。

后置数学知识

• 向量内积定义 : $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\times \cos\langle\vec{a},\vec{b}\rangle$
• 向量内积坐标表示 : $(x_1,y_1)\cdot(x_2,y_2)=x_1x_2+y_1y_2$

数据范围约定

「本题采用捆绑测试」

• Subtask1( $20\%$ ) : $r_1=r_2=r_3$
• Subtask2( $40\%$ ) : $r_1,r_2,r_3 \le 10$
• Subtask3( $40\%$ ) : $r_1,r_2,r_3 \le 10^9$

对于 $100\%$ 的数据 $0 < r_1 \le r_2 \le r_3 \le 10^9$