题目背景

小 W 学习了一种叫做线段树的数据结构。

题目描述

很快，小 W 就发现：线段树实在是太浪费空间了！

比如，一棵 $n=6$ 的线段树长下面这样：

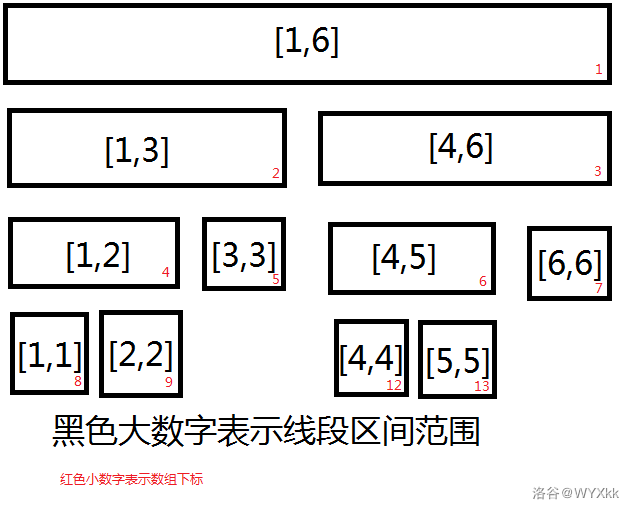
可以发现，只有 $11$ 个节点存储了有用信息，但使用的数组下标到了 $13$。

令 $f(n)$ 表示一棵 $n$ 个叶子节点的线段树所占的最大数组下标，现在小 W 想让你求出：

其中，$\oplus$ 表示异或运算，相当于 C++ 中的^符号。

输入格式

一行两个整数，表示 $l,r$，意义如上。

输出格式

一行一个整数，表示结果。

6 6

13

提示

样例解释

$f(6)=13$，故答案为 $13$。

提示

如果你不知道什么是线段树：

void build(int k,int l,int r)
{
	if(l==r)
	{
		//do something
		//e.g. tree[k]=a[l]
		return;
	}
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
	//do something
	//e.g. tree[k]=tree[k<<1]+tree[k<<1|1]
}

翻译成人话就是：编号为 $k$ 节点有一个线段 $[l,r]$，如果 $l\neq r$，那么令 $mid=\lfloor\dfrac{l+r}2\rfloor$，它有两个子节点，左儿子编号为 $2k$，线段为 $[l,mid]$；右儿子编号为 $2k+1$，线段为 $[mid+1,r]$，然后在子节点上递归建树。

调用build(1,1,n)后就建好了一棵线段树，即编号为 $1$ 的结点的线段为 $[1,n]$。

数据范围

对于 $10\%$ 的数据，$1\le l\le r\le10^3$。
对于 $40\%$ 的数据，$1\le l\le r\le 10^6$。
对于 $100\%$ 的数据，$1\le l\le r\le10^{15}$，答案在long long范围内。