题目描述

给定一个 $2^n \times 2^n$ 的矩阵，最开始每个格子都是白色的。格子的颜色可以是白色或黑色。定义一个矩阵的价值为：

1. 如果矩阵是单色的，则它的价值为 $1$ 金币；
2. 否则，将矩阵分割成 $4$ 个大小相等的子矩阵，矩阵的价值为子矩阵的价值之和加 $1$ 金币。

给定 $q$ 个询问，每个询问给定一个行/列的编号 $x$，你需要改变这一行/列中每个格子的颜色（黑色变为白色，白色变为黑色），然后计算出改变之后的新矩阵的价值。

输入格式

第一行包含两个整数 $n$ 和 $q \ (0 \leq n \leq 20, 1 \leq q \leq 10^6)$，代表矩阵的大小为 $2^n \times 2^n$ 以及有 $q$ 个询问。

接下来 $q$ 行每行包含两个整数 $t$ 和 $x \ (0 \leq t \leq 1, 1 \leq x \leq 2^n)$。如果 $t=0$，则改变第 $x$ 行的颜色；否则，改变第 $x$ 列的颜色。

输出格式

对于每个询问，输出一行答案。

2 7
1 3
0 2
1 1
1 4
0 4
0 3
1 1

13
17
21
17
21
17
13

提示

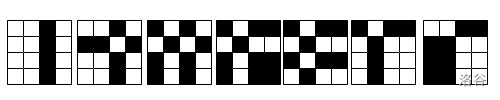
样例中，每个询问后的矩阵如下图所示：