题目背景

一个风和日丽的早晨，小 $\mathrm{S}$ 带着他的好朋友小 $\mathrm{A}$ 在小树林里面数树。

看着满树林的树，小 $\mathrm{S}$ 灵感一闪，想到了一道题目。

---

$$\mathrm{Suddenly,\ Little\ S\ thought\ of\ a\ supercalifragilisticexpialidocious\ problem.} $$$$\mathrm{He\ wanted\ Little\ A\ to\ answer\ it.}$$

题目描述

现在有 $n$ 个点，每个点有一个权值 $v_i$。

小 $\mathrm{S}$ 想要小 $\mathrm{A}$ 从中选一些点组成一个集合，设集合 $S=\{d_1,d_2,\dots,d_m\}(1\leq m\leq n)$。

当然，小 $\mathrm{A}$ 还需要保证这些点能形成一颗树，且 $d_i$ 的度数为 $v_{d_i}(i\in[1,m])$。

• 节点的度数：与它相邻的节点的个数。

小 $\mathrm{S}$ 想问小 $\mathrm{A}$ 有多少种满足条件的方案。

小 $\mathrm{A}$ 深知自己肯定不会这道题目，所以他就拿来问你了。

由于方案数可能很大，所以请对 $998244353$ 取模。

输入格式

第一行，一个整数 $n$。

第二行，$n$ 个整数 $v_1,v_2,\dots,v_n$

输出格式

一行一个整数，表示方案数。

3
1 1 1

3

5
1 2 1 3 1

8

8
1 2 1 2 4 1 3 1

44

50
8 1 10 2 2 1 2 1 1 2 5 1 11 6 13 13 10 4 1 13 11 2 2 11 13 10 1 1 4 3 4 2 15 2 2 1 1 2 1 7 14 2 2 4 13 2 7 5 6 10 

176873472

提示

---

样例说明

• 对于样例 $1$，在三个节点中任选两个即可，答案为 $C^{2}_{3}=3$。

• 对于样例 $2$，如图，共有 $8$ 种选择节点的方法。

---

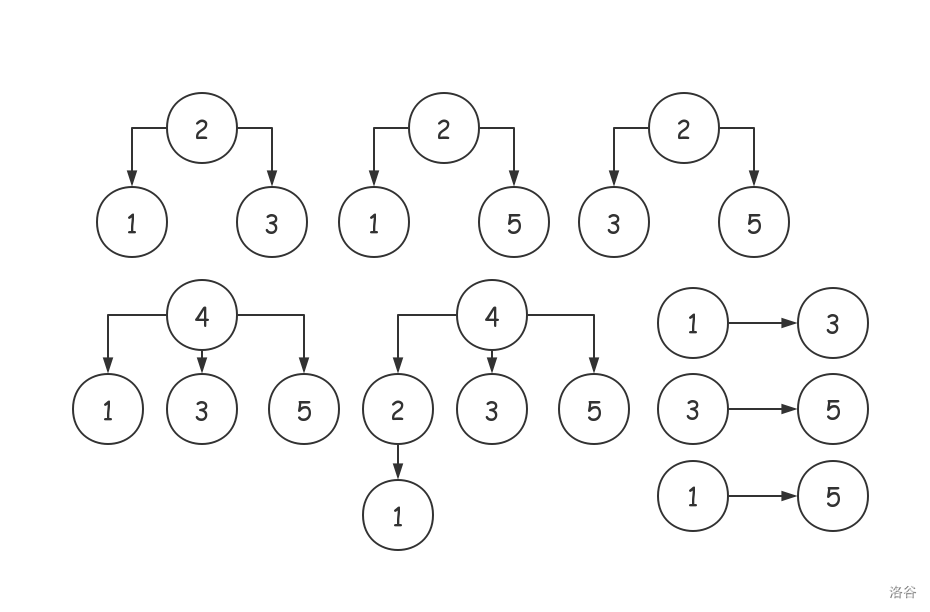
数据范围与约定

本题使用捆绑测试。

Subtask 编号	$n\leq$	特殊性质	得分
$1$	$20$	无	$11$
$2$	$50$		$12$
$3$	$300$		$10$
$4$	$2500$		$17$
$5$	$4\times 10^4$		$6$
$6$	$3\times 10^5$	$v_i\leq 3$	$8$
$7$		数据随机	$7$
$8$	$5\times 10^5$	无	$29$

对于 $100\%$ 的数据，$2 \leq n \leq 5 \times 10^5$，$\ 1 \leq v_i \leq n$。

---

$\mathrm{Subtask\ 7}$ 中“数据随机”指：对于所有 $v_i$，$\frac{1}{3}$ 的概率为 1，$\frac{2}{3}$ 的概率为 $[2,n]$ 中等概率选择一个数。

---

对于前 $4$ 个 $\mathrm{Subtask}$，时间限制 $1\mathrm{s}$。

对于第 $5$ 个 $\mathrm{Subtask}$，时间限制 $3\mathrm{s}$。

对于后 $3$ 个 $\mathrm{Subtask}$，时间限制 $6\mathrm{s}$。

对于所有测试点，空间限制 $256\mathrm{MB}$。