题目背景

滥用本题评测将封号

注：本题按照传统题方式进行评测，即，你的程序需要包含 main 函数。

题目描述

Kenan 为沿着巴库大街某一侧的建筑和天桥绘制了一张规划图。规划图中有 $n$ 栋建筑，从 $0$ 到 $n-1$ 编号。还有 $m$ 座天桥，从 $0$ 到 $m-1$ 编号。这张规划图绘制在一张二维平面上，其中建筑和天桥分别是垂直和水平的线段。

第 $i$（$0 \le i \le n-1$） 栋建筑的底部坐落在坐标 （$x[i],0$） 上，建筑的高度为 $h[i]$。因此，它对应一条连接点 （$x[i],0$） 和 （$x[i],h[i]$） 的线段。

第 $j$（$0 \le j \le m-1$） 座天桥的两端分别在第 $l[j]$ 栋建筑和第 $r[j]$ 栋建筑上，并具有正的 $y$ 坐标 $y[j]$。因此，它对应一条连接点 （$x[l[j]],y[j]$） 和 （$x[r[j]],y[j]$） 的线段。

称某座天桥和某栋建筑相交，如果它们有某个公共的点。因此，一座天桥在它的两个端点处与两栋建筑相交，同时还可能在中间和其他建筑相交。

Kenan 想要找出从第 $s$ 栋建筑的底部到第 $g$ 栋建筑的底部的最短路径长度，或者确认这样的路径不存在。在这里行人只能沿着建筑和天桥行走，并且不允许在地面上行走，也就是说不允许沿着 $y$ 坐标为 $0$ 的水平线行走。

行人能够在任意交点从某座天桥走进某栋建筑，或者从某栋建筑走上某座天桥。如果两座天桥的端点之一在同一点上，行人也可以从其中一座天桥走上另一座天桥。

你的任务是帮助 Kenan 回答他的问题。

实现细节

你需要实现下列函数。 int64 min_distance(int[] x,int[] h,int[] l,int[] r,int[] y,int s,int g)

• $x$ 和 $h$：长度为 $n$ 的整数数组。
• $l$、$r$ 和 $y$：长度为 $m$ 的整数数组。
• $s$ 和 $g$：两个整数。
• 如果从第 $s$ 栋建筑的底部到第 $g$ 栋建筑的底部的最短路径存在，则该函数应该返回最短路径的长度。否则，该函数应该返回-1。

输入格式

• 第 $1$ 行：$n$，$m$。
• 第 $2+i$ 行（$0 \le i \le n-1$）：$x[i]$，$h[i]$。
• 第 $n+2+j$ 行（$0 \le j \le m-1$）：$l[j]$，$r[j]$，$y[j]$。
• 第 $n+m+2$ 行：$s$，$g$。

输出格式

共一行，为函数 min_distance 的返回值。

7 7
0 8
3 7
5 9
7 7
10 6
12 6
14 9
0 1 1
0 2 6
0 6 8
2 3 1
2 6 7
3 4 2
4 6 5
1 5

27

提示

样例说明

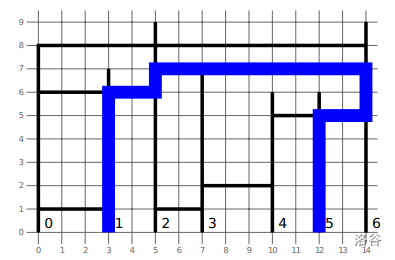
限制条件

• $1 \le n,m \le 10^5$。
• $0 \le x[0] < x[1] < \cdots < x[n-1] \le 10^9$。
• $1 \le h[i] \le 10^9$（对于所有 $0 \le i \le n-1$）。
• $0 \le l[j] \le r[j] \le n-1$（对于所有 $0 \le j \le m-1$）。
• $1 \le y[j] \le \min(h[l[j]],h[r[j]])$（对于所有 $0 \le j \le m-1$）。
• $0 \le s,g \le n-1$。
• $s ≠ g$。
• 除在端点处外，任意两座天桥不会有其他公共的点。

子任务

1. （$10$ 分）$n,m \le 50$。
2. （$14$ 分）每座天桥最多与 $10$ 栋建筑相交。
3. （$15$ 分）$s=0$，$g=n-1$，且所有建筑的高度相等。
4. （$18$ 分）$s=0$，$g=n-1$。
5. （$43$ 分）没有任何附加限制。