题目描述

将一个 8 $\times$ 8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 $(n-1)$ 次后，连同最后剩下的矩形棋盘共有 $n$ 块矩形棋盘。 (每次切割都只能沿着棋盘格子的边进行)

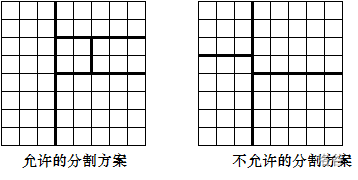
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成 $n$ 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差 $\sigma = \sqrt{ \frac{ \sum_{i=1}^n (x_i - \bar x)^2 } { n }}$ ，其中平均值 $\bar x = \frac{\sum_{i=1}^n x_i}{n}$ , $x_i$ 为第 $i$ 块矩形棋盘的分。

请编程对给出的棋盘及 $n$ ，求出 $\sigma$ 的最小值。

输入格式

第一行为一个整数 $n$ ($1 < n< 15$)。

第二行至第九行每行为 $8$ 个小于 $100$ 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式

仅一个数，为 $\sigma$ （四舍五入精确到小数点后三位）。

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

1.633