题目背景

小 $\mathrm{A}$ 找到了一张藏宝图。

他顺着藏宝图上的路线来到了一扇古老的大门前，门上有六芒星的图案。

他把手轻轻地放在六芒星上……

霎时间，六芒星光芒大放，四周亮如白昼。

（新增一组大样例）

题目描述

小 $\mathrm{A}$ 面前出现了 $10^{1000}$ 扇门，每个门上都写着它自己的编号，分别为 $1,2,3,\dots,10^{1000}$。

这时，守门人小 $\mathrm{M}$ 向小 $\mathrm{A}$ 走来。

“这些门，并不普通，它有魔力。”

“我会给你一些区间 $l,r$，请你求出区间 $[l,r]$ 里所有门的魔力值之和与魔力值之积。”

“因为结果可能很大，请你将结果 $mod\ p$。 ”

“如果你正确地回答了所有询问，你将会拥有这扇门后的所有宝藏。”

“哦，对了，一扇门的魔力值就是其在二进制下 $1$ 的个数。”

简单来说，记第 $i$ 扇门的魔力值为 $d_i$，给定的区间为 $[l,r]$，请求出：

$$\sum_{l}^{r}d_i\bmod\ p \quad \prod_{l}^{r}d_i\bmod\ p $$

由于门的数量实在太多，小 $\mathrm{A}$ 决定向你请求帮助。

输入格式

第一行三个正整数 $T,p,n$（$n$ 会在数据范围中说明）。

接下来 $T$ 行，第 $i$ 行两个正整数 $l_i,r_i$。

输出格式

输出 $T$ 行，每行 $2$ 个数，由空格隔开，第 $i$ 行分别为：

$$\sum_{l}^{r}d_i\bmod\ p \quad \prod_{l}^{r}d_i\bmod\ p $$

7 1000000007 0
3 7
1 10
1 1048576
20180815 20180830
20180632 20180639
123456789 987654321
123456789987654321 123456789987654321123456789987654321

10 24
17 96
10485761 64327945
255 803716286
124 290111979
996409842 54001814
253678327 263109263

提示

---

样例说明

数据 $1$：

$$\sum_{3}^{7}d_i=2+1+2+2+3=10$$ $$\prod_{3}^{7}d_i=2\times 1\times 2\times 2\times 3=24 $$

数据 $2$：

$$\sum_{1}^{10}d_i=1+1+2+1+2+2+3+1+2+2=17$$ $$\prod_{1}^{10}d_i=1\times 1\times 2\times 1\times 2\times 2\times 3\times 1\times 2\times 2=96 $$

---

数据范围与约定

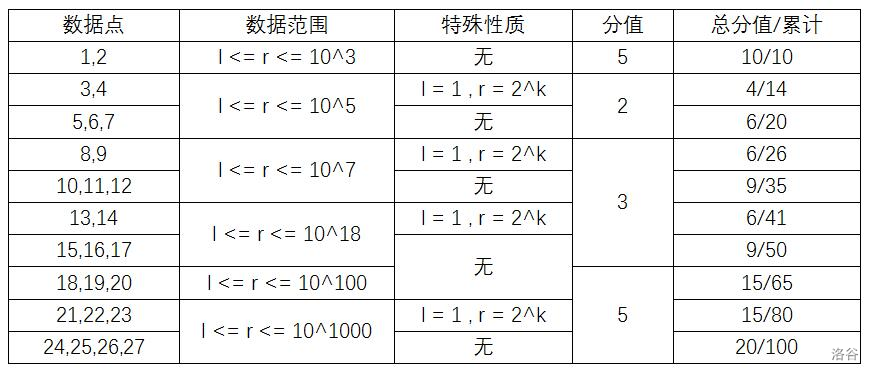
为了方便拿部分分，输入格式中的 $n$ 为该测试点的编号。

所有具有特殊性质的测试点一共 $31\%$。

对于 $100\%$ 的数据，有 $1\leq n\leq 27,1\leq T \leq 10,10^9 \leq p \leq 1.001\times 10^9,1\leq l\leq r\leq 10^{1000}$，保证 $p$ 为质数。

---

对于测试点 $1-20$，时限 $300ms$，剩下的 $7$ 个测试点时限 $2s$。

对于所有测试点，空间限制 $256MB$

---

“吱嘎”一声，封尘千年的大门缓缓打开。

刺眼的金光照了出来……