题目背景

公元 $3100$ 年，地球联盟的银河系内 $N$ 个星球已经完成了道路大建设，从原来的 $N-1$ 条双向时空隧道变成了无向完全图。

Louis Paosen 是一个星际旅行家，上次你虐队的时候顺便帮他解决了难题，于是他又来请求你帮忙啦。

题目描述

仍然是出于资金的考虑，地球联盟没能将所有的道路都建造得尽善尽美。通过某条道路对于飞船的性能有一定的要求。

Louis Paosen 在联盟内举办了盛大的 kfc 三人篮球赛，一时间，许多来自不同星球的选手纷纷赶来参赛。

整个地球联盟的内部正在热卖三种飞船 (A/B/C 类)，由于收了广告费的缘故，组队的时候要求 $3$ 人中第一人使用 A，第二人使用 B，第三人使用 C (这样可以获得加分)。

现在有许许多多个三人小组准备参赛，他们准备好了飞船(符合加分条件)，但是他们可能来自不同的星球，由于飞船性能的限制，他们可能无法一起到达某个星球。

由于这三家公司制造工艺大相径庭，飞船对同一条道路环境的耐受力区别很大，而有奇怪的规律。

点 $u$ 有三组系数 $P_A[u],P_B[u],P_C[u]$ ，边 $u\leftrightarrow v$ 的通过难度为:

当一个飞船的性能指数不低于某条边对应种类的通过难度时,这个飞船才能够通过 (具体见样例解释)。

Louis Paosen 在每个星球上都准备了比赛点，所以你只要对每个三人小组，给出其可行的集合点个数就好了。

输入格式

第一行：$n,q$。

第 2~4 行：$P_A[1\sim n],P_B[1\sim n],P_C[1\sim n]$。

后 $q$ 行：每行六个数 $h_A,u_A,h_B,u_B,h_C,u_C$ ，表示一个三人小队中每个人的飞船性能以及出发星球编号。

输出格式

对于每个三人小队，输出一行一个数，回答可行的集合点个数。

3 3
1 2 3
3 2 1
4 2 2
5 1 2 2 3 3
3 3 3 3 3 3
6 3 5 2 3 1

2
2
1

10 10
43 24 8 66 96 25 43 87 62 8 
80 25 94 72 43 18 94 96 11 54 
19 25 92 87 76 36 89 91 69 22 
82 2 82 5 82 3
70 10 96 8 70 8
52 7 23 5 52 10
85 1 62 4 85 5
1 5 49 7 1 6
32 7 54 8 32 9
6 1 89 4 6 10
82 10 38 5 82 7
87 2 1 10 87 2
12 3 77 5 12 8

10
7
0
5
0
1
1
5
1
1

提示

• 性质①：$P_C[1\sim n]$ 都相等；
• 性质②：$P_B[1\sim n]$ 都相等；
• 性质③：$P_A[1\sim n], P_B[1\sim n], P_C[1\sim n]\in \{0,1\}$。

（#1~#9 每个 $6$ 分，#10~#13 共 $46$ 分；#1~#7 空间限制为 500MB，其余测试点空间限制为 125MB）。

所有输入中的数都是 $[0,10^8]$ 内的整数。

样例 1 解释

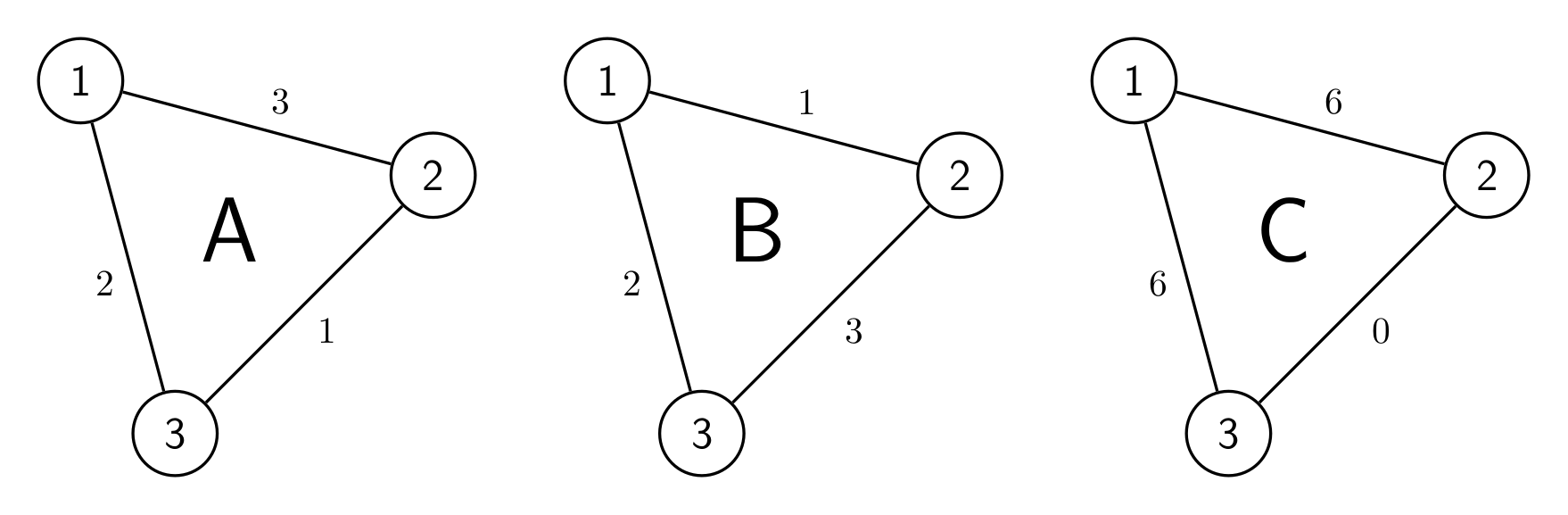
三张性能图如上。

如 A 图，$\begin{cases}(1,2)=P_A[1]\ {\rm xor}\ P_A[2]=3;\\(1,3)=P_A[1]\ {\rm xor}\ P_A[3]=2;\\(2,3)=P_A[1]\ {\rm xor}\ P_A[2]=1;\end{cases}$

(边的产生方式就是根据三个数组异或)

第一组人:

• 从 $1$ 出发的 A 飞船性能高达 $5$，能到达所有的星球。
• 从 $2$ 出发的 B 飞船性能仅为 $2$，不能经过$(3,2)=3$，但是还能到达所有的星球。
• 从 $3$ 出发的 B 飞船性能仅为 $3$，只能经过$(2,3)=0$，能到达 $2,3$ 号星球。
• 综上，第一组所有人都能到达的星球有 $2$ 个。