#P5140. 树枝修剪
树枝修剪
Description
的花园里有一颗常年没有修剪的树,这一天, 家里来了客人,为了给客人一个好印象,他需要整理这个花园,但是那一颗树显得太碍眼了,他必须要给他好好地修剪一下。
这是一颗以为根的有根树,有个节点。 在根节点, 对某些叶子的形态感到不满,需要剪去多余的枝条。
有个需要修剪的叶子节点,这些叶子节点有一些多余的枝条,这些叶子节点有着自己的权值,表示这个节点上有多少个 不需要的枝条。同时,因为花园里没法容下这些枝条(否则就变得不和谐了), 需要把这些枝条安装到某些节点上。
有一个神奇的胶水和一把神奇的剪刀,因此你不需考虑每个树枝的固定形态,根据 的推测,一共有个叶子节点需要安装这些枝条,这些节点有各自的权值,表示需要个枝条才能把这棵树变得很好看。
为了修剪好这棵树, 不得不在树上跑边,把每个叶子节点中多余的枝条剪下,并用胶水粘在其他的有需要的叶子节点上。每条边都有不同的长度,现在,由于树太过庞大, 需要知道,他最少需要跑多远的路才能使这棵树被修剪好, 也要回到树根上下来。
虽然 有这些神奇的工具,但他的口袋是有限的,容量为, 不能一次带太多枝条,即不能超过,这更使他懒于考虑这些繁琐的问题。 当然会算啦,他那么巨,但他为了养足精力去剪枝条,这一艰巨的任务就落在你身上了。
已经把心中树的形状告诉你了,他要躺在椅子上看你怎么算这些问题。
Input Format
输入的第一行个整数:.
接下来行描述每个树边,每行个整数:表示与有一条长度为的边。
接下来一行个整数:;
接下来行,每行两个整数:,表示在第个节点有个多余枝条,数据保证为叶子节点。
接下来行,每行两个整数:,表示在第个节点需要个枝条,数据保证为叶子节点。
数据保证
Output Format
一行,一个整数,表示 最少需要跑多长的路才能把树修剪好并回到树根爬下树。
4 2 1
2 1 4
4 1 2
3 1 2
1 2
2 6
3 3
4 3
40
5 1 1
1 2 2
3 2 2
4 1 2
5 4 2
1 1
3 1
5 1
16
20 10 18
1 17 86406
17 16 94583
19 10 28177
16 18 31981
10 14 36241
1 7 28919
2 1 94673
5 6 2801
7 11 81927
11 13 7779
17 5 71948
19 7 20264
1 8 17736
13 20 97181
17 9 16807
11 15 93705
17 3 29601
1 12 43829
13 4 27537
1 6
20 23585
9 8376
12 3128
15 5417
8 4011
3 1156
6 1497
1289613990
Hint
样例1解释:
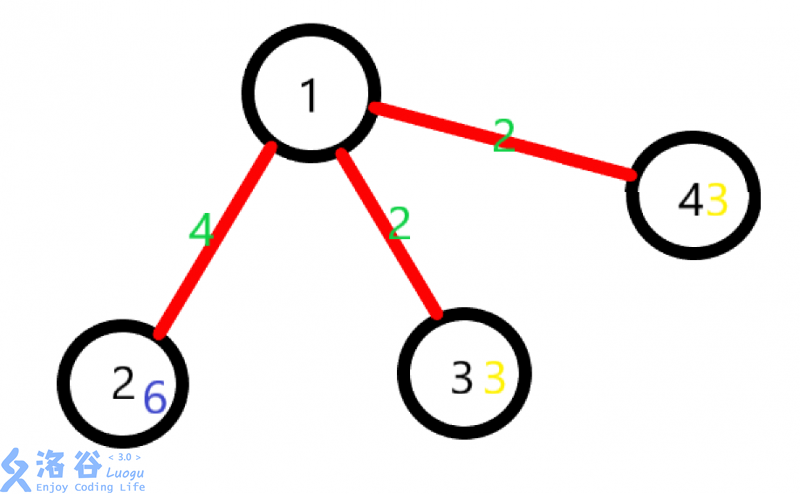
蓝色数字表示有多少多余枝条,黄色数字表示需要的枝条数。
则最优方案为:,答案为;
对于的数据,为样例1。
对于的数据,
对于的数据,$n\leq 40,0000,G\leq 1000;S+T\leq n;a_{i},b_{i}\leq 10^{9};w\leq 10^{9}$
数据保证不会有任意一个叶子节点既需要枝条又有多余枝条。

 京公网安备 11011102002149号
京公网安备 11011102002149号