题目描述

You travel through a scenic landscape consisting mostly of mountains – there are $n$ landmarks (peaks and valleys) on your path. You pause for breath and wonder: which mountain are you currently seeing on the horizon?

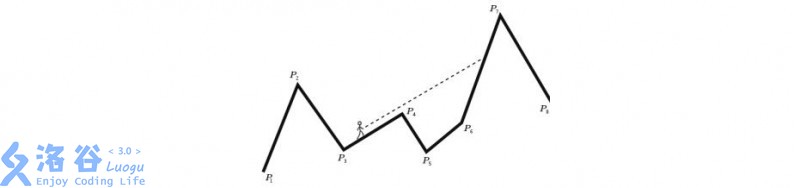
Formally: you are given a polygonal chain $P_1,P_2,\cdots,P_n$ in the plane. The $x$ coordinates of the points are in strictly increasing order. For each segment $P_i P_{i+1}$ of this chain, find the smallest index $j > i$, for which any point of $P_j P_{j+1}$ is visible from $P_i P_{i+1}$ (lies strictly above the ray $P_i \ P^{\rightarrow}_{i+1}$).

输入格式

The first line of input contains the number of test cases $T$. The descriptions of the test cases follow:

The first line of each test case contains an integer $n(2 \le n \le 100 000)$ – the number of vertices on the chain.

Each of the following $n$ lines contains integer coordinates $x_i, y_i$ of the vertex $P_i (0 \le x_1 < x_2 < \cdots < x_n \le 10^9, 0 \le y_i \le 10^9)$.

输出格式

For each test case, output a single line containing $n-1$ space-separated integers. These should be the smallest indices of chain segments visible to the right, or $0$ when no such segment exists.

题目大意

• 给定平面内一个由点依次连接起来形成的折线 $P_1,P_2,\cdots,P_n$，保证 $x$ 坐标递增。
• 对于折线上的所有线段，找到最小的 $j>i$，使得存在一个在 $P_jP_{j+1}$ 上的点可以被 $P_iP_{i+1}$ 上的任何一个点看到，也就是严格在射线 $P_iP_{i+1}$ 上方。若没有，输出 $0$.
• 多组数据。

$2\le n\le 10^5$，坐标均在 $10^9$ 以内。

2
8
0 0
3 7
6 2
9 4
11 2
13 3
17 13
20 7
7
0 2
1 2
3 1
4 0
5 2
6 1
7 3

0 3 6 5 6 0 0
6 4 4 0 6 0