题目描述

在平面直角坐标系上有 $n$ 个点，其中第 $i$ 个点的坐标是 $(x_i,y_i)$ ，所有点在一个以 $(0,0)$ 和 $(A,B)$ 为相对顶点的矩形内。

如果 $x_i=0$ ，那么我们称这个点在西侧。如果 $x_i=A$ ，那么我们称这个点在东侧。

这些点之间有 $m$ 条边，每条边可能是有向边也可能是无向边，保证边在交点以外的任何地方不相交。

现在请你求出，对于每一个西侧的点，能够沿着边到达多少东侧的点。

输入格式

第一行四个空格隔开的数 $n,m,A,B$ 。

接下来 $n$ 行，每行两个空格隔开的数 $x_i,y_i$ 。

接下来 $m$ 行，每行三个空格隔开的数 $c_i,d_i,k_i$​​ ，表示一条 $c_i$​​ 和 $d_i$ 之间的边。如果 $k_i=1$ ，那么表示这条边是有向边，方向为 $c_i$​​ 指向 $d_i$​​ ，否则这条边是无向边。

输出格式

输出有若干行，每行一个数表示答案。请按照 $y$ 从大到小的顺序输出所有点对应的答案。

5 3 1 3
0 0
0 1
0 2
1 0
1 1
1 4 1
1 5 2
3 5 2

2
0
2

12 13 7 9
0 1
0 3
2 2
5 2
7 1
7 4
7 6
7 7
3 5
0 5
0 9
3 9
1 3 2
3 2 1
3 4 1
4 5 1
5 6 1
9 3 1
9 4 1
9 7 1
9 12 2
10 9 1
11 12 1
12 8 1
12 10 1

4
4
0
2

提示

样例 $2$ 解释

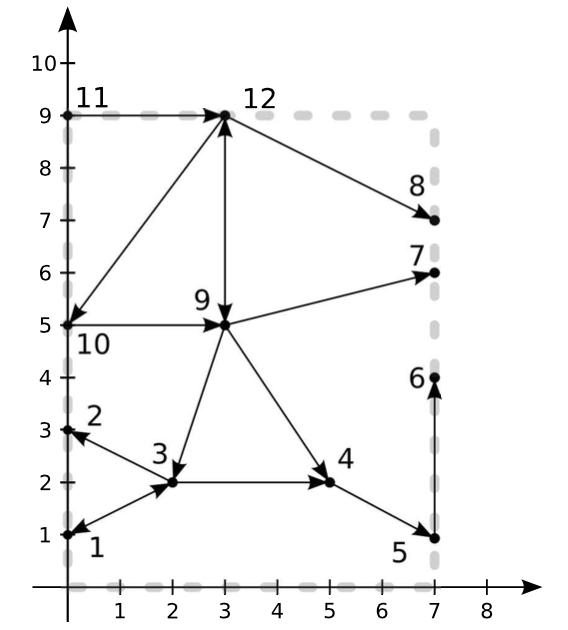
数据范围

对于 $100\%$ 的数据，有 $1\le n\le 300\ 000;0\le m\le 900\ 000;1\le A,B\le 10^9;0\le x_i\le A;0\le y_i\le B;1\le c_i,d_i\le n;k_i\in \{1,2\}$。保证西侧的点至少有一个，保证每一个无序对 $\{c_i,d_i\}$ 只会出现一次。