题目描述

阿Q博士正在观察一个圆形器皿中的粒子运动。不妨建立一个平面直角坐标系，圆形器皿的圆心坐标为$(x_0, y_0)$，半径为$R$。器皿中有若干个粒子，假设第$i$个粒子在时刻$0$的位置为$(x_i, y_i)$，速度为$(v_{x_i},v_{y_i})$（注：这是一个速度向量，若没有发生碰撞，$t$时刻的位置应该是$(x_i + t * v_{x_i}, y_i + t * v_{y_i})$ ）。假设所有粒子的运动互不干扰；若某个粒子在某个时刻碰到了器皿壁，将发生完全弹性碰撞，即速度方向按照碰撞点的切线镜面反射，且速度大小不变（如图）。认为碰撞是瞬间完成的。

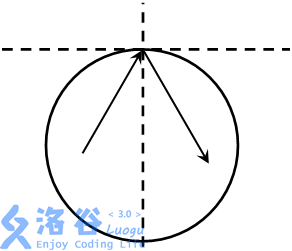
尽管碰撞不会影响粒子的速率，但是粒子却会受到一定的伤害，所以若某一个粒子碰撞了$k$次器皿壁，那么在第$k$次碰撞时它便会消亡。

出于研究的需要，阿Q博士希望知道从时刻$0$到所有粒子都消亡这段时间内，所有粒子之间的最近距离是什么。你能帮助他么？

输入格式

输入文件particle.in第一行包含三个实数，分别为$x_0, y_0, R$，即圆形器皿的圆心坐标及半径。第二行包含两个正整数$N, k$，分别表示粒子的总数与消亡碰撞次数。接下来$N$行每行四个实数，分别为$x_i, y_i, v_{x_i} , v_{y_i}$，保证$(x_i, y_i)$都在圆内且$(v_{x_i}, v_{y_i})$非零。

输出格式

输出文件particle.out仅包含一个实数，即所有粒子的历史最近距离，精确到小数点后三位。

0 0 10
2 10
0 -5 0 1
5 0 1 0

7.071

提示

对于所有的数据，$2 \leq N \leq 100$。$1 \leq k \leq 100$。

请注意实数精度问题。