题目描述

为了简单期间，投影屏幕对应二维平面中的一条平行与 $x$ 轴，连接点 $(x_1^s,y^s)$ 和点 $(x_2^s,y^s)$ 的线段。

JYY 的投影仪位于原点，朝向 $y$ 轴正方向，发出对称于 $y$ 轴并且张角度数为 $ang$ 的光束（$ang$ 是角度制），如图所示（粗线条为投影屏幕，黄色区域为投影仪射出的光束）。

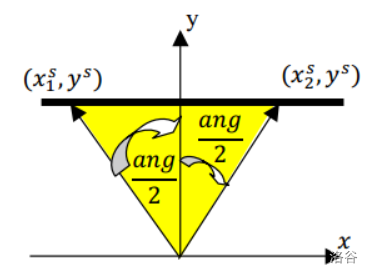
实验室内一共有 $n$ 的障碍物，每个障碍物都对应于二维平面中的一条线段（我们认为这些障碍物的厚度为 $0$）。

有一些障碍物是不能反光的，因此光线只要射到这些线段上，就会被完全吸收（比如投影屏幕就是不会反光的）；其他障碍物则是双面可以反光的，光线如果射到这些线段上，就会按照基本光学原理进行反射。

所有的障碍物都相互不接触，并且也不会与投影屏幕，或者坐标原点接触。

光线在空气中传播会有损耗，因此在 JYY 的实验室中，光线在传播了 $len$ 的距离之后，就会消失。

现在 JYY 想知道，投影屏幕上被照亮的区域占投影屏幕总长度的比率。

输入格式

第一行一个正整数和两个正实数，为 $N,ang,len$。

接下来 $n$ 行，每行 $5$ 个整数 $x_1,x_2,y_1,y_2,r$，表示 JYY 的实验室内存在一个连接点 $(x_1,y_1)$ 和点 $(x_2,y_2)$ 的障碍物，$r$ 为 $0$ 或者 $1$。当 $r=0$ 时表示这个障碍物不反光，$r=1$ 则表示这个障碍物双面反光。

接下来一行四个整数 $x_1^s,y^s,x_2^s,y^s$，表示投影屏幕的位置，保证第二个和第四个整数相同。

输出格式

一行一个 $0$ 到 $1$ 之间的实数，表示屏幕上被照亮部分的长度与屏幕总长的比值，结果精确到小数点后 $4$ 位。

2 150.0000 1000.0000
-60 165 50 165 0
110 25 130 120 1
-205 360 275 360

0.7443

提示

样例解释 1

如图。

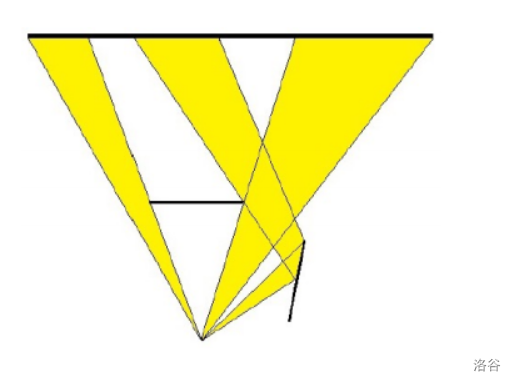
数据范围

对于 $100\%$ 的数据，$0\leq n\leq 10,0<ang\leq 150,0<len\leq 10^3$，任意输入坐标绝对值不超过 $10^3$。

输入数据保证 $y^s>0,x_1^s<x_2^s$，并且对于任意障碍物满足 $\vert y_2\vert<y^s$。

输入数据还保证对于一条光线在消失或被吸收之前至多反射 $30$ 次。