#P4536. [CQOI2007] 三角形
[CQOI2007] 三角形
Description
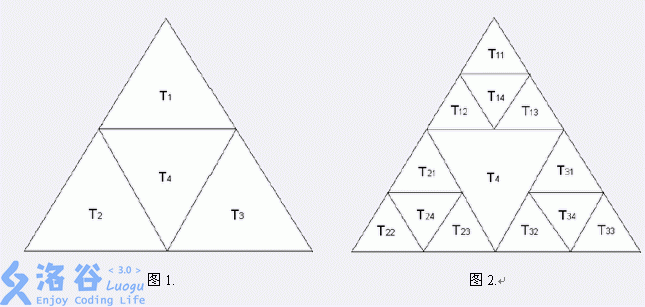
Draw an equilateral triangle and connect the midpoints of its three sides to obtain four triangles, denoted , as shown in Figure 1.
Apply the same subdivision to the first three triangles to obtain smaller triangles: $T_{11}, T_{12}, T_{13}, T_{14}, T_{21}, T_{22}, T_{23}, T_{24}, T_{31}, T_{32}, T_{33}, T_{34}$, as shown in Figure 2.
Continue subdividing the triangles whose indices end with ... The resulting fractal is called the Sierpinski triangle.
If triangle does not contain triangle , and one entire edge of is a part of an edge of , then we say “rests on” an edge of . For example, rests on and , but does not rest on .
Given a triangle in the Sierpinski triangle, find all the triangles it “rests on”.
Input Format
The input contains a single line: the index of a triangle. It starts with T followed by digits from to . Only the last digit may be .
Output Format
Output one triangle index per line, sorted in lexicographical ascending order.
T312
T314
T34
T4
Hint
Constraints: For of the testdata, .
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号