#P4502. [ZJOI2018] 保镖
[ZJOI2018] 保镖
Description
Jiutiao Kelian is a playful girl.
When a cute girl goes out to play with friends, danger may arise. So Kelian’s father secretly stationed bodyguards to protect her from the shadows. Because Kelian is strong-willed, her father does not want her to notice the many bodyguards around her, so the bodyguards must regularly rotate their posts to avoid being discovered.
An ideal rotation is: the bodyguards far from Kelian are moved closer, and the ones close to Kelian are moved farther. After some planning, the bodyguards will rotate according to the following rules:
- During rotation, Kelian and the bodyguards’ positions can be abstracted as points in a 2D Cartesian plane. Let Kelian’s position be , a bodyguard’s position be , and the position after rotation be .
- Before and after rotation, the relative direction between each bodyguard and Kelian remains the same. That is, for , lies on the ray .
- Before and after rotation, the distance between each bodyguard and Kelian becomes the reciprocal of the original. That is, for , .
Meanwhile, Kelian’s safety level is determined by the bodyguards’ positions. The more bodyguards on the outside, the more information they can observe, and the safer Kelian is. Therefore, we define the number of vertices of the convex hull of the bodyguards’ positions as Kelian’s safety level.
However, Kelian’s whereabouts are unpredictable. On this day, the bodyguards lost track of her and only know that next time she will appear inside the rectangle with lower-left corner and upper-right corner , with a uniform distribution over this rectangle (i.e., equally likely). Since it has been a long time since the last rotation, they plan to rotate when Kelian appears next. Also, with a very small probability, Kelian may appear at exactly the same location as some bodyguard. In that case, that bodyguard will be discovered and will remain still, while the other bodyguards still rotate according to the rules above.
Now, Kelian’s father wants to compute the expected value of Kelian’s safety level (the number of convex hull vertices) after the rotation.
If you are not familiar with convex hulls, here is a formal definition:
- A simple polygon is a convex polygon if and only if the line segment between any two interior points lies entirely inside it.
- For a point set , its convex hull is the convex polygon of minimum area that contains all points and has no three consecutive vertices collinear.
Input Format
- The first line contains an integer , the number of bodyguards.
- The second line contains four integers , describing the rectangle where Kelian may appear.
- Each of the next lines contains two integers , the coordinates of a bodyguard. All bodyguards’ positions are pairwise distinct.
Output Format
Output a single real number: the expected number of vertices of the convex hull.
Your answer will be accepted if its absolute or relative error is within .
4
0 0 1 1
0 0
2 0
0 1
1 1
3.7853981633974474
Hint
Sample Explanation
Here we draw the situation when Kelian appears at , as shown below. Bodyguards 1, 2, and 4 keep their positions, denoted . Bodyguard 3 moves from to with coordinates .
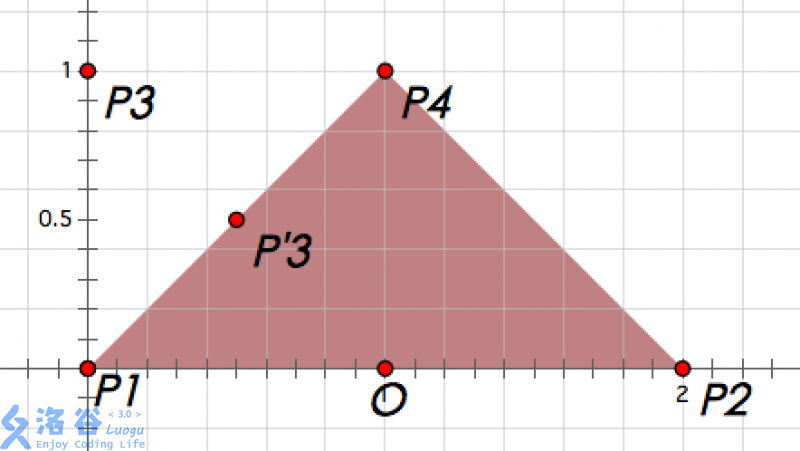
At this moment, the convex hull of is the triangle , so Kelian’s safety level is 3. Note that lies exactly on edge , but by the definition of the convex hull, it is not a vertex.
Constraints
| 测试点 | 测试点 | ||
|---|---|---|---|
| 1 | 6 | ||
| 2 | 7 | ||
| 3 | 8 | ||
| 4 | 9 | ||
| 5 | 10 |
For 100% of the testdata, it is guaranteed that , , , and .
For 100% of the testdata, the bodyguards’ positions are pairwise distinct.
To avoid possible precision issues, in all actual testdata and large samples, the width and height of the rectangle where Kelian may appear are at least , i.e., .
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号