#P4142. 洞穴遇险
洞穴遇险
Description
{{The entire cave is an grid. Each cell is denoted as , where . Here is the row index from top to bottom, and is the column index from left to right. is the top-left corner, is the top-right corner, is the bottom-left corner, and is the bottom-right corner.
Cells with odd have an instability , while cells with even have instability .
ZRQ happens to have pillars that can support the cave. The strength of each pillar can be regarded as infinite.
As long as a cell is supported, its instability becomes .
Each pillar is L-shaped: in addition to occupying its current cell (the corner), it must also occupy two adjacent cells so that the three cells form an L shape. You can place it in any of the orientations.
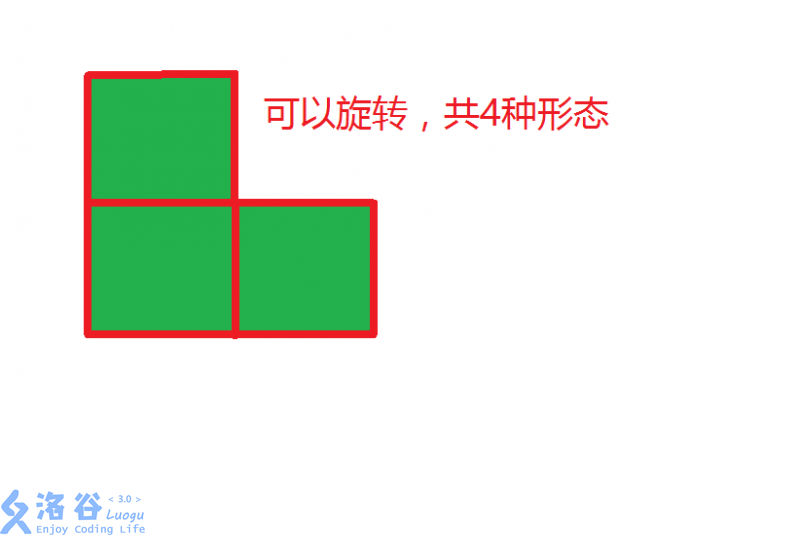
Occupying adjacent cells with a pillar does not reduce their instability (in other words, a pillar only has force at its corner cell).
Some cells have already collapsed, so you cannot place a pillar there, and these cells cannot be occupied either. There are such cells. Their instability is (even if is odd, a collapsed cell’s instability is still ).
ZRQ asks: after placing some pillars (you do not have to use all pillars), what is the minimum possible sum of instabilities?}}
Input Format
{{The first line contains three integers .
The next lines each contain integers, representing the instability of each cell. It is guaranteed that cells with even and collapsed cells have instability .
The next lines each contain two integers , denoting the coordinates of the collapsed cells.}}
Output Format
{{Output a single integer: the minimum possible sum of instabilities.}}
3 3 1
0 1 0
2 0 1
0 1 0
1 3
3
3 3 4
0 2 0
0 0 4
0 3 0
1 3
2 1
2 2
3 1
9
Hint
{{There are test points, each worth points, for a total of points.
Constraints:
- For test points –: .
- For test points –: .
- For test points –: .
- For all test points: , , .
Sample #1 explanation: It is clearly impossible to have any two unstable cells both covered by a pillar’s corner. Therefore, just cover with a pillar’s corner. The remaining instability is .
Sample #2 explanation: None can be placed. The remaining instability is .}}
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号