#P4007. [清华集训 2017] 小 Y 和恐怖的奴隶主
[清华集训 2017] 小 Y 和恐怖的奴隶主
Description
Xiao Y is an OIer who likes playing games. One day, she is playing a game and needs to fight a Boss.
Although this Boss has HP, it only brings one minion — a "Terrifying Slave Owner" with exactly HP.
This "Terrifying Slave Owner" has a special skill: whenever it takes damage but does not die (death means HP ), and the number of the Boss's minions is less than the cap , it summons a new "Terrifying Slave Owner" with HP.
Now Xiao Y can make attacks. Each time she attacks, she chooses uniformly at random one target from the set consisting of the Boss and all of the Boss's minions, and reduces that target's HP by . She wants to know the expected total HP deducted from the Boss after attacks. To avoid precision issues, your answer should be taken modulo .
Input Format
The first line contains three positive integers , where is the number of queries, and are as defined in the statement.
Then follow lines. Each line contains a positive integer , representing a query asking for the expected HP deducted from the Boss after attacks.
Output Format
Output lines. For each query, output a non-negative integer — the answer modulo .
It can be proven that the desired expectation is a rational number. Suppose it equals . Then the number you output should satisfy .
3 2 6
1
2
3
499122177
415935148
471393168
Hint
[Sample 1 Explanation]
For the first query, the first attack has probability to hit the Boss and probability to hit the minion, so the answer is . .
For the second query: if the first attack hits the Boss, then there is probability that the second attack still hits the Boss and probability that it hits the minion; if the first attack hits the minion, then a new minion (the "Terrifying Slave Owner") is summoned, so there is probability that the second attack hits the Boss and probability that it hits a minion. Therefore the answer is $\frac{1}{2}\times\frac{1}{2}\times2+\frac{1}{2}\times\frac{1}{2}\times1+\frac{1}{2}\times\frac{1}{3}\times1+\frac{1}{2}\times\frac{2}{3}\times0 = \frac{11}{12}$. .
[Tips]
The order of problems may not correspond to difficulty.
[Subtasks]
Across all test points, $1 \leq T \leq 1000, 1 \leq n \leq {10}^{18}, 1 \leq m \leq 3, 1 \leq k \leq 8$.
The scores and Constraints for each test point are as follows:
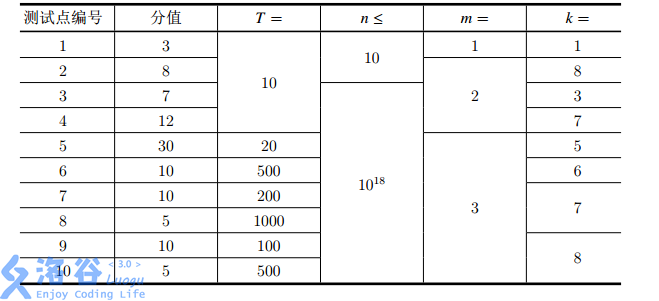
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号