Description

The inspiration for this problem comes from the following data:

This data follows the “description method” rule: on the $n+1$-th layer, describe the data of the $n$-th layer from left to right. The rule is as follows: starting from the first datum, whenever you encounter a run of $a_1$ consecutive $b_1$, write $a_1\,b_1$ as two new data at the end of the $n+1$-th layer (the “end” here means appended after the last datum; if the $n+1$-th layer has no data yet, then this “end” is the beginning). Then, immediately describe the next run of $a_2$ consecutive $b_2$ ($b_1 \neq b_2$), and so on, until all data have been fully described. At that point, the $n+1$-th layer is constructed. Here $n$ is a positive integer.

Now, I have a new idea. Given an initial datum $Q$ (the initial datum is on the first layer, and the first layer contains only one datum — the initial datum $Q$), construct a data array using a rule similar to the one above (the description method), called the “Langze Array.” My rule is: on odd-numbered layers follow rule $A$, and on even-numbered layers follow rule $B$. See the figure below:

The above shows part of the Langze Array when the initial datum is $1$. As for what the exact rules are, that is for you to explore.

However!!!

That is not the final goal. What I want you to find is: on the $i$-th layer, how many $x$ are there (we define the layer containing the initial datum as the first layer)?

Input Format

The input contains only one line with three integers $Q$, $i$, and $x$, separated by single spaces.

$Q$ is the initial datum of the Langze Array.

Output Format

Output a single line with one integer: the count of $x$ on the $i$-th layer.

Since the output can be large, output the result modulo $20171111$ (that is, take the remainder after dividing the original result by $20171111$).

2 2 2

1

2 14 5

12

Hint

Sample 1 explanation:

A (small) part of the constructed Langze Array is:

Therefore, the count of $2$ on the $2$-nd layer is $1$.

Notes:

• All data are integers.

• If you have no idea how to proceed, you may choose to solve some subproblems first.

• Constraints for each test point are as follows:

  

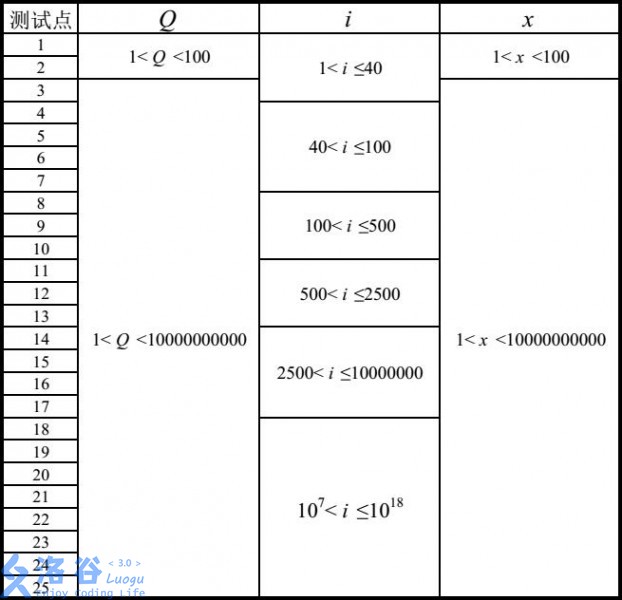
Translated by ChatGPT 5