Description

A graph $\text G$ is an undirected connected graph with no self-loops, and there is at most one edge between any two vertices. We define the shortest path between vertices $v$ and $u$ as a path from $v$ to $u$ that uses the fewest edges. Every vertex that lies on some shortest $v$-$u$ path is called a $v$-$u$ Geodetic vertex, and the set of these vertices is denoted by $I(v,u)$.

We call the set $I(v,u)$ a Geodetic set.

For example, in the figure below, $I(2,5)=\{2,3,4,5\}$, $I(1,5)=\{1,3,5\}$, and $I(2,4)=\{2,4\}$.

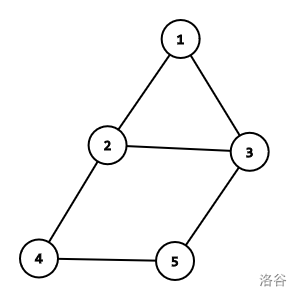
Given a graph $\text G$ and several pairs $v, u$, please compute $I(v,u)$ for each pair.

Input Format

The first line contains two integers $n, m$, representing the number of vertices and edges of $\text G$ (vertices are numbered $1 \sim n$).

The next $m$ lines each contain two integers $a, b$, indicating that there is an undirected edge between vertices $a$ and $b$.

The $(m+2)$-th line contains an integer $k$, representing the number of given pairs.
The next $k$ lines each contain two integers $v, u$, the start and end vertices of each pair.

Output Format

Output $k$ lines. For each pair $v, u$ in the input, output in one line all vertex indices in $I(v,u)$ in increasing order of vertex indices.

5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4

2 3 4 5
1 3 5
2 4

Hint

For all testdata, $1 \le n \le 40$, $1 \le m, k \le \frac{n(n-1)}{2}$.

Translated by ChatGPT 5