#P3840. Simurgh 西默夫
Simurgh 西默夫
题目背景
【不支持提交】
时间:3s
空间:1024MB
题目描述
根据沙纳玛(Shahnameh)中的古代波斯传说,Zal,传奇的波斯英雄,疯狂地爱上了Kabul王国的公主Rudaba。在Zal向Rudaba求婚时,Rudaba的父亲给他了一个挑战。
在波斯有个城市,标记为从到,以及条双向道路,标记为从到。 每条道路连接两个不同的城市。每一对城市至多会被一条道路连接。有些道路是御道__(royal roads)__,专用于皇室行驶,但这是保密的。Zal的任务是找出哪些道路是御道。
Zal有一张包括所有城市和所有道路的波斯地图。他不知道哪些道路是御道,但是他可以求救于Simurgh——好心的神鸟、Zal的保护者。然而,Simurgh并不想直接告诉他哪些道路是御道。作为替代,Simurgh告诉Zal,所有御道的集合是一个黄金集合__(golden set)__。一个道路的集合是黄金集合,当且仅当:
-
它恰好包含条道路,而且
-
对于每一对城市,仅沿着这个集合中的道路即可从其中一个城市抵达另外一个城市。
此外,Zal可以问Simurgh一些问题。对于每个问题:
-
Zal选出道路的一个黄金集合,然后
-
Simurgh会告诉Zal,在所选择的黄金集合中有多少条道路是御道。
你的程序可以问Simurgh最多个问题,以此帮助Zal找出御道的集合。评测工具将扮演Simurgh的角色。
实现细节
你需要实现下面的函数:
(Java) int[] find\_roads(int n, int[] u, int[] v)
(C++) std::vector<int> find\_roads(int n, std::vector<int> u, std::vector<int> v)
-
:城市的数量,
-
和:均为长度为的数组。对于所有,和是被道路所连接的城市。
-
该函数需要返回一个长度为的数组,其中包括了所有御道的标号(可以以任意的顺序给出)。
你的程序至多只能调用评测工具中的如下函数次:
(Java) int count\_common\_roads(int[] r)
(C++) int count\_common\_roads(std::vector<int> r)
-
:长度为的数组,其中包括了一个黄金集合中的道路标号(可以以任意的顺序给出)。
-
该函数将返回中的御道数量。
输入格式
你需要实现上述函数
输出格式
函数需要返回一个合法的结果
n = 4
u = [0, 0, 0, 1, 1, 2]
v = [1, 2, 3, 2, 3, 3]
一个可能的输出:
[0, 1, 5]
提示
下面是一个例子
find\_roads(4, [0, 0, 0, 1, 1, 2], [1, 2, 3, 2, 3, 3])
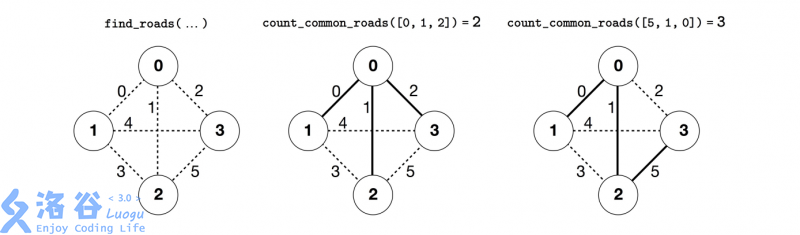
这个例子中有个城市和条道路。我们将连接城市和的道路表示为。这些道路按照下面的顺序被标为从到:,,,,和。每个黄金集合包含条道路。
假设御道是标号为,和的道路,即,和。这样的话:
-
count\_common\_roads([0, 1, 2])返回。该询问涉及到标号为和的道路,即,和。其中有两条道路是御道。 -
count\_common\_roads([5, 1, 0])返回。该询问涉及到所有的御道。
函数find\_roads需要返回[5, 1, 0]或任意其他包含这三个元素且长度为的数组。
注意,下面列出的调用是不允许的:
-
count\_common\_roads([0, 1]):这里的长度不是。 -
count\_common\_roads([0, 1, 3]):这里不是一个黄金集合,因为无法仅沿道路,,就从城市走到城市。
限制条件
-
-
(对于所有)
-
对于所有,道路连接两个不同的城市(即)。
-
每对城市之间至多连有一条道路。
-
经由这些道路,可以在任意一对城市之间来往。
-
所有的御道组成一个黄金集合。
-
find\_roads可以调用count\_common\_roads最多次。在每次调用中,由所给出的道路必须是一个黄金集合。
子任务
-
(分),
-
(分),
-
(分),
-
(分),在任意两个城市之间都连有一条道路
-
(分)

 京公网安备 11011102002149号
京公网安备 11011102002149号