Description

Arezou and her brother Borzou are twins. Their birthday present is a fun toy train set. They built a railway system with $n$ stations and $m$ directed tracks. The stations are numbered from $0$ to $n - 1$. Each track starts at some station and ends at the same station or another station. Every station has at least one outgoing track.

Some stations are charging stations. Whenever the train arrives at a charging station, it is fully recharged. A fully charged train has enough power to traverse $n$ tracks in a row; without recharging, it will stop right before entering the $(n + 1)$-st track.

Each station has a track switch that can be set to any one of its outgoing tracks. When the train departs a station, it follows the track currently selected by that station’s switch.

The twins plan to play a game with their train. They have divided the stations between them: each station belongs either to Arezou or to Borzou. There is only one train in the game. At the start, the train is at station $s$ and fully charged. To start the game, the owner of station $s$ sets its switch to one of its outgoing tracks. Then they start the train, and it begins moving along the tracks. Whenever the train enters a station for the first time, the owner of that station must set its switch. Once a switch is set, it remains fixed until the game ends. Therefore, if the train visits a station again, it will leave along the same track as before.

Since the number of stations is finite, the train’s movement will eventually enter a cycle. A cycle is a sequence of distinct stations $c_0, c_1, \dots, c_{k - 1}$ such that after leaving station $c_i$ for $0 \leqslant i < k - 1$ the train takes the track to $c_{i + 1}$, and after leaving $c_{k - 1}$ it takes the track to $c_0$. A cycle may consist of a single station ($k = 1$), i.e., the train leaves station $c_0$ and immediately takes the track back to $c_0$.

If the train can keep running forever, Arezou wins. Otherwise, the train will eventually run out of power and stop, so Borzou wins. In other words, if there is at least one charging station among $c_0, c_1, \dots, c_{k - 1}$ so that the train can keep getting recharged and run around the cycle forever, then Arezou wins. Otherwise, even if the train loops several times, it will eventually run out of power, and Borzou wins.

You are given such a railway system. Arezou and Borzou will play $n$ rounds. In round $s$ ($0 \leqslant s \leqslant n - 1$), the train initially starts at station $s$. Your task is to determine, for each round, whether Arezou wins no matter how Borzou plays.

Implementation details:

You need to implement the following function:

(C++) std::vector<int> who_wins(std::vector<int> a, std::vector<int> r, std::vector<int> u, std::vector<int> v)

(Java) int[] who_wins(int[] a, int[] r, int[] u, int[] v)

• $a$: an array of length $n$. If Arezou owns station $i$, then $a[i] = 1$; otherwise Borzou owns station $i$, and $a[i] = 0$.
• $r$: an array of length $n$. If station $i$ is a charging station, then $r[i] = 1$; otherwise $r[i] = 0$.
• $u$ and $v$: arrays of length $m$. For every $0 \leqslant i \leqslant m - 1$, there is a directed track that starts at $u[i]$ and ends at $v[i]$.
• The function should return an array $w$ of length $n$. For every $0 \leqslant i \leqslant n - 1$, if in the game starting at station $i$ Arezou can win regardless of how Borzou plays, then $w[i] = 1$. Otherwise, $w[i] = 0$.

Input Format

You need to implement the subroutine described above.

Output Format

Your subroutine must return a valid result.

a = [0, 1]
r = [1, 0]
u = [0, 0, 1, 1]
v = [0, 1, 0, 1]

who_wins = [1, 1]

Hint

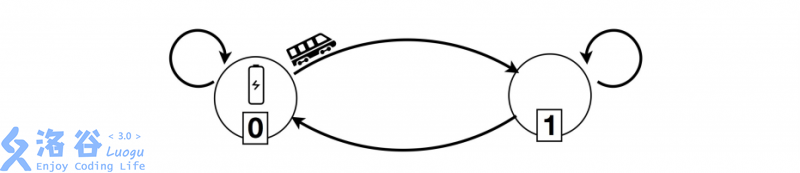
• There are 2 stations. Station 0 is a charging station owned by Borzou. Station 1 is owned by Arezou and is not a charging station.
• There are 4 directed tracks: (0, 0), (0, 1), (1, 0), and (1, 1), where (i, j) denotes a track from station i to station j.
• Consider the game starting at station 0. If Borzou sets station 0’s switch to (0, 0), the train will loop there forever (note that station 0 is a charging station). In this case, Arezou wins. Otherwise, if Borzou sets station 0’s switch to (0, 1), then Arezou can set station 1’s switch to (1, 0). The train will then loop between the two stations. Arezou still wins because station 0 is a charging station, so the train runs forever. Therefore, regardless of how Borzou plays, Arezou wins.
• By a similar argument, in the game starting at station 1, Arezou also wins no matter how Borzou plays. Therefore, the function should return [1, 1].

Constraints

• $1 \leqslant n \leqslant 5000$.
• $n \leqslant m \leqslant 20000$.
• There is at least one charging station.
• Every station has at least one outgoing track.
• It is possible that a track starts and ends at the same station (i.e., $u[i] = v[i]$).
• All tracks are pairwise distinct. That is, there do not exist indices $i$ and $j$ ($0 \leqslant i < j \leqslant m - 1$) such that $u[i] = u[j]$ and $v[i] = v[j]$.
• For all $0 \leqslant i \leqslant m - 1$, $0 \leqslant u[i], v[i] \leqslant n - 1$.

Subtasks

1. (5 points) For all $0 \leqslant i \leqslant m - 1$, $v[i] = u[i]$ or $v[i] = u[i] + 1$.
2. (10 points) $n \leqslant 15$.
3. (11 points) Arezou owns all stations.
4. (11 points) Borzou owns all stations.
5. (12 points) The number of charging stations is $1$.
6. (51 points) No additional constraints.

Translated by ChatGPT 5