#P2305. [NOI2014] 购票
[NOI2014] 购票
Description
This summer, NOI celebrated its 30th anniversary in SZ City. OIers from cities across the country will depart from their homes to attend the event in SZ City.
All cities form a rooted tree with SZ City as the root, and each city is connected to its parent by a road. For convenience, we number the cities with integers from to , where the number of SZ City is . For any city other than SZ City, we are given its parent city in this tree and the length of the road to its parent.
To travel from city to SZ City, the method is as follows: choose an ancestor of city , pay for a ticket, and take a vehicle to . Then choose an ancestor of city , pay, and reach . Repeat this process until you arrive at SZ City.
For any city , we are given a distance limit for its transportation. For an ancestor of city , city can reach with a single ticket if and only if the total length of all roads along the path between them does not exceed ; otherwise, it cannot reach with a single ticket.
For each city , we are also given two non-negative integers as fare parameters. If the total length of all roads from city to city is , then the price of the ticket from city to city is .
OIers in each city want to minimize the total amount of money spent on tickets when traveling to SZ City. Your task is to tell the OIers in each city their minimum total cost.
Input Format
The first line contains two non-negative integers , denoting the number of cities and the testdata type (its meaning is mentioned in “Hint”).
The next lines each describe a city other than SZ City. Specifically, line contains five non-negative integers , denoting the parent city of city , the length of the road to its parent, the two fare parameters, and the distance limit, respectively.
Note: The input does not include SZ City with number . Lines describe cities to .
Output Format
The output contains lines, each with an integer.
The -th line gives the minimum total ticket cost to reach SZ City starting from city .
Likewise, note that SZ City with number is not included in the output.
7 3
1 2 20 0 3
1 5 10 100 5
2 4 10 10 10
2 9 1 100 10
3 5 20 100 10
4 4 20 0 10
40
150
70
149
300
150
Hint
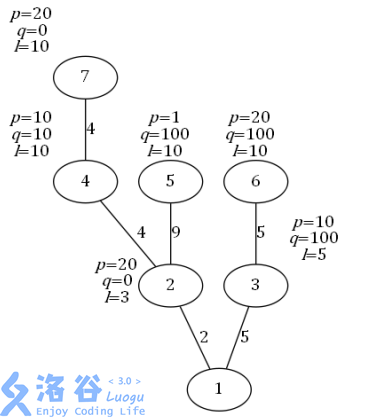
The routes from each city to SZ City are as follows (an arrow denotes a single direct trip):
City : Can only choose , with cost .
City : Can only choose , with cost .
City : Since , it can choose . If choosing , the cost is ; if choosing , the cost is . Therefore, choose .
City : Can only choose , with cost . It cannot choose because , while the total distance from city to city is , so city cannot reach city directly.
City : If choosing , the cost is ; if choosing , the cost is . Therefore, choose .
City : Choose , with cost .
All other options are worse than this plan.
Constraints
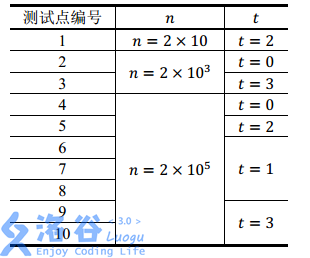
For all testdata, , , , , , and the total path length from any city to SZ City does not exceed .
The input denotes the testdata type, , where:
- When or , for all cities in the input, , i.e., all cities form a chain ending at SZ City.
- When or , for all cities in the input, , i.e., there is no distance limit, and every city can reach all of its ancestors.
- When , the testdata has no special property.
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号