#P2173. [ZJOI2012] 网络
[ZJOI2012] 网络
Description
There is an undirected graph . Each node has a weight, and each edge has a color. This undirected graph satisfies the following two conditions:
-
For any node, among all edges incident to it, there are at most two edges of the same color.
-
There is no monochromatic cycle in the graph, i.e., no cycle formed by edges of the same color.
On this graph, you need to support the following three operations:
-
0 x ymeans set the weight of node to . -
1 u v wmeans change the color of edge to . -
2 c u vmeans query, in the subgraph formed by edges of color , the maximum weight among all nodes that lie on any simple path from to .
Input Format
The first line contains four positive integers , denoting the number of nodes, the number of edges, the number of colors, and the number of operations, respectively.
The next lines each contain one positive integer , the weight of node .
The next lines each contain three positive integers , denoting an edge connecting nodes and with color .
The last lines each contain several positive integers, representing one operation.
Output Format
Output several lines, each containing the corresponding message.
-
For node weight modification operations, no output is required.
-
For edge color modification operations, print one of the following:
-
If there is no edge connecting node and node , print
No such edge.. -
If the modification would violate condition 1, do not modify the edge color and print
Error 1.. -
If the modification would violate condition 2, do not modify the edge color and print
Error 2.. -
Otherwise, modify the edge color successfully and print
Success..
Only print the first applicable message. That is, if both conditions 1 and 2 would be violated, print only Error 1..
- For query operations, print one integer as the answer. If there is no path of color between and , print .
4 5 2 7
1
2
3
4
1 2 0
1 3 1
2 3 0
2 4 1
3 4 0
2 0 1 4
1 1 2 1
1 4 3 1
2 0 1 4
1 2 3 1
0 2 5
2 1 1 4
4
Success.
Error 2.
-1
Error 1.
5
Hint
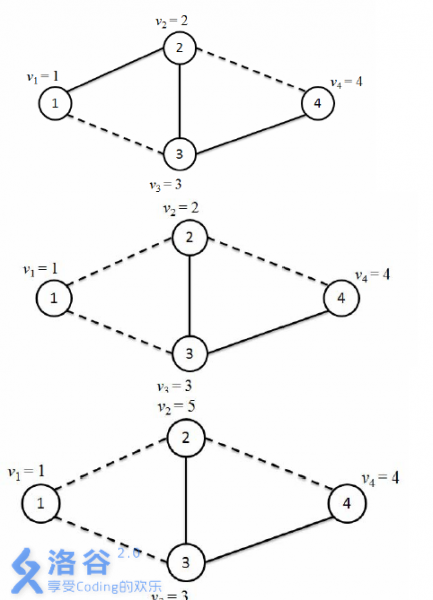
Edges of color are solid; edges of color are dashed.
In the subgraph formed by edges of color , there is a path from node to node : . Thus .
Changing the edge between nodes and to color succeeds, so print Success..
Changing the edge between nodes and to color would create a monochromatic cycle of color (), violating condition 2, so do not modify it and print Error 2..
There is no path of color from node to node , so print .
Changing the edge between nodes and to color would make node incident to three edges of color , violating condition 1, so do not modify it and print Error 1..
Change the weight of node to .
In the subgraph formed by edges of color , there is a path from node to node : . Thus .
Constraints
- For of the testdata: , , .
- Additionally, for of the testdata: , , , .
- For of the testdata: , , , .
, . There are no multiple edges or self-loops in the graph.
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号