Description

Xiao W is the manager of a newly built cemetery. The cemetery can be regarded as an $N×M$ rectangle. Each lattice point is either planted with an evergreen tree, or is a grave plot that has not yet been assigned.

The local residents are very devout Christians, and they are willing to choose a suitable grave plot for themselves in advance. To show their sincerity to the Lord, they hope their grave plot has a high level of piety.

The piety of a grave plot is defined as the number of crosses centered at this plot. A cross consists of a center grave plot, and exactly $k$ evergreen trees immediately above, below, left, and right of it.

Formally, for a grave plot at coordinates $(x, y)$, the number of crosses centered at it is the number of sequences of length $4k$ of ordered pairs $[(x_{1,1},y_{1,1}),\allowbreak(x_{1,2},y_{1,2}),\allowbreak\cdots,(x_{1,k},y_{1,k}),\allowbreak(x_{2,1},y_{2,1}),\allowbreak(x_{2,2},y_{2,2}),\allowbreak\cdots,(x_{2,k},y_{2,k}),\allowbreak(x_{3,1},y_{3,1}),\allowbreak(x_{3,2},y_{3,2}),\allowbreak\cdots,(x_{3,k},y_{3,k}),\allowbreak(x_{4,1},y_{4,1}),\allowbreak(x_{4,2},y_{4,2}),\allowbreak\cdots,(x_{4,k},y_{4,k})]$ that satisfy:

• Each ordered pair corresponds to the coordinates of an evergreen tree.
• $x_{1,1}<x_{1,2}<\cdots< x_{1,k}<x$ and $y_{1,1}=y_{1,2}=\cdots=y_{1,k}=y$.
• $x<x_{2,1}<x_{2,2}<\cdots< x_{2,k}$ and $y_{2,1}=y_{2,2}=\cdots=y_{2,k}=y$.
• $y_{3,1}<y_{3,2}<\cdots< y_{3,k}<y$ and $x_{3,1}=x_{3,2}=\cdots=x_{3,k}=x$.
• $y<y_{4,1}<y_{4,2}<\cdots< y_{4,k}$ and $x_{4,1}=x_{4,2}=\cdots=x_{4,k}=x$.

Xiao W wants to know the sum of the piety levels of all grave plots in the cemetery.

Input Format

The first line contains two positive integers $N$ and $M$, representing the width and length of the cemetery. Therefore, this rectangular cemetery has $(N+1) ×(M+1)$ lattice points, with the lower-left corner at $(0, 0)$ and the upper-right corner at $(N, M)$.

The second line contains a positive integer $W$, representing the number of evergreen trees in the cemetery.

From the third line, there are $W$ lines. Each line contains two non-negative integers $x_i$ and $y_i$, representing the coordinates of an evergreen tree. The input guarantees that no two evergreen trees have the same coordinates.

The last line contains a positive integer $k$, as defined in the statement.

Output Format

Output a single non-negative integer, which is the sum of the piety levels over all grave plots in this cemetery. For convenience, output the answer modulo $2{,}147{,}483{,}648$.

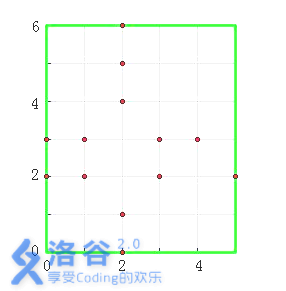
5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2

6

Hint

In the figure, the number of crosses centered at grave plots $(2, 2)$ and $(2, 3)$ is $3$, so their piety levels are both $3$. The piety level of every other grave plot is $0$.

For $30\%$ of the testdata, $1 ≤ N, M ≤ 10^3$.

For $60\%$ of the testdata, $1 ≤ N, M ≤ 10^6$.

For $100\%$ of the testdata, $1 ≤ N, M ≤ 10^9$，$0 ≤ x_i ≤ N$，$0 ≤ y_i ≤ M$，$1 ≤ W ≤ 10^5$，$1 ≤ k ≤ 10$。

There exists $50\%$ of the testdata such that $1 ≤ k ≤ 2$.

There exists $25\%$ of the testdata such that $1 ≤ W ≤ 10^4$.

Translated by ChatGPT 5