Description

Trees can be used to represent evolutionary relationships among species. An "evolutionary tree" is a tree with edge weights, where each leaf node represents a species, and the distance between two leaves represents the difference between the two species. Now, an important problem is to reconstruct the corresponding "evolutionary tree" from the distances between species.

Let $N=\{1,2,3,\cdots ,n\}$, and use a matrix $M$ on $N$ to define a tree $T$. The matrix $M$ satisfies: for any $i$, $j$, $k$, we have $M[i,j]+M[j,k] \ge M[i,k]$. The tree $T$ satisfies:

1. The leaves are the elements of $N$.
2. All edge weights are non-negative integers.
3. $d_T(i,j)=M[i,j]$, where $d_T(i,j)$ denotes the length of the shortest path between $i$ and $j$ in the tree.

As shown below, the matrix $M$ describes a tree.

$$M=\begin{bmatrix} 0 & 5 & 9 & 12 & 8 \\ 5 & 0 & 8 & 11 & 7 \\ 9 & 8 & 0 & 5 & 1 \\ 12 & 11 & 5 & 0 & 4 \\ 8 & 7 & 1 & 4 & 0 \\ \end{bmatrix}$$

The weight of a tree is the sum of all edge weights in the tree. For any valid matrix $M$, the total weight of the tree it represents is uniquely determined. It is impossible to find two trees with different total weights that are both consistent with $M$. Your task is to compute the weight of the tree represented by the given matrix $M$. The figure below shows one tree represented by the above matrix $M$, and the total weight of this tree is $15$.

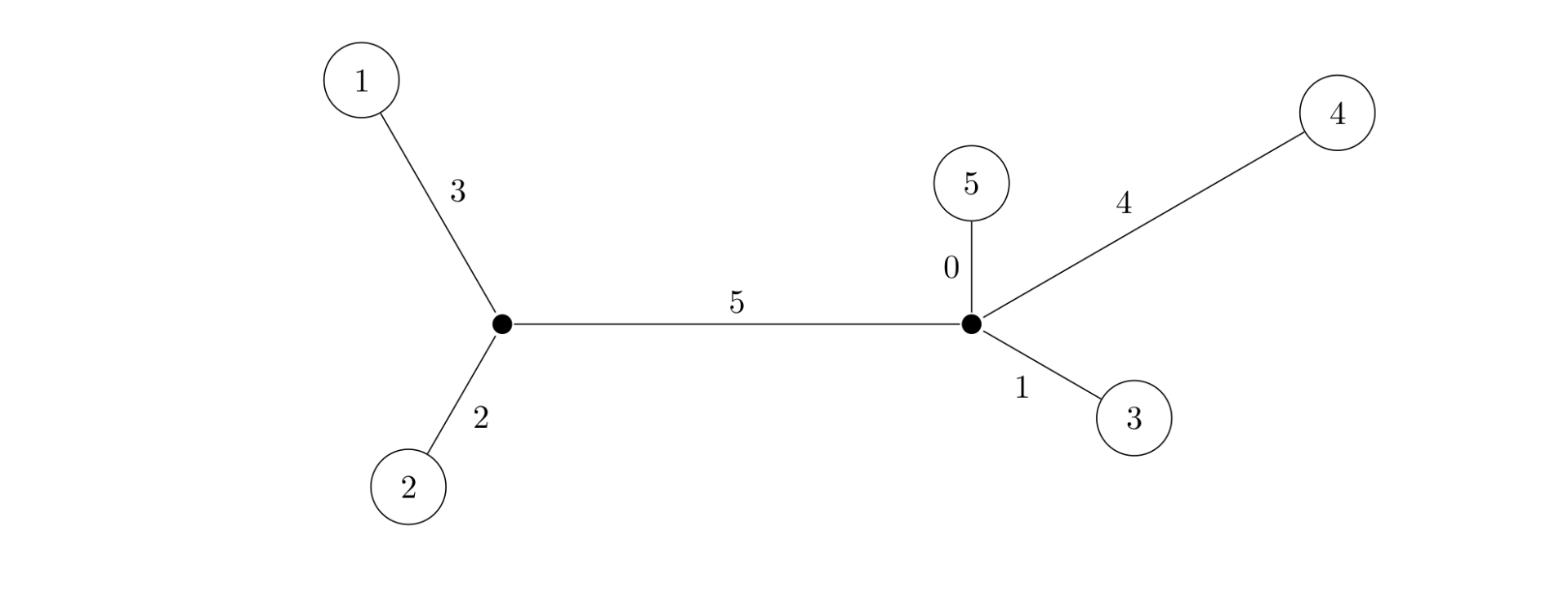
Input Format

The first line contains an integer $n$ with $2<n<30$.

Then $n-1$ lines follow, giving the strict upper triangular part of matrix $M$ (excluding the diagonal). All entries in the matrix are non-negative integers not exceeding $100$. The input is guaranteed to be valid. Matrix $M$ is symmetric with zeros on the diagonal. On the $i$-th of the next $n-1$ lines ($1 \le i \le n-1$), there are $n-i$ integers: $M[i, i+1], M[i, i+2], \ldots, M[i, n]$.

Output Format

Output one line containing a single integer, the total weight of the tree.

5
5 9 12 8
8 11 7
5 1
4

15

4
15 36 60
31 55
36

71

Hint

Translated by ChatGPT 5