说明

A 国和 B 国正在划分一块 $n\times m$ 的矩形土地。

显然，这块土地上有 $(n-1)$ 条水平线和 $(m-1)$ 条垂直线。

给这 $(n+m-2)$ 条线分配 $[1,k]$ 间的整数。定义一个格子的权值为在它左/上方的线上整数之和减去在它右/下方的线上整数之和。

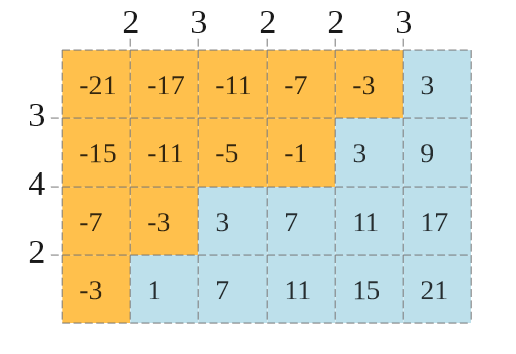
给定每个格子权值的要求（要求这个格子的权值 $\lt 0$ 或者 $\gt 0$）。在 $k^{n+m-2}$ 种分配整数的方案中，求出有多少个方案符合要求。

只需要输出答案对 $(10^9+7)$ 取模后得到的结果。

输入格式

第一行，三个正整数 $n,m,k$。

接下来一个 $n\times m$ 的矩阵，里面的元素不是 $\texttt{+}$ 就是 $\texttt{-}$，表示每个格子权值符号的要求。

输出格式

输出一行一个整数，表示答案。

4 6 4
-----+
----++
--++++
-+++++

2364

3 3 2
--+
--+
-++

2

2 3 2
---
+++

0

提示

对于 $100\%$ 的数据，保证 $1\le n,m,k\le 80$。

特殊性质 A：$(i,j)$ 要求为 $\texttt{+}$，当且仅当 $i+j\ge m+1$。