#P11082. [ROI 2019] 高速电车 (Day 1)
[ROI 2019] 高速电车 (Day 1)
Description
计划部门打算考虑几个不同的高速电车路线方案。每个方案由一个目标站点和预计行驶时间来定义。然而,部门知道实际的行驶时间可能无法完全符合预期。因此,他们使用参数 来评估路线的可行性:对于给定的预计时间 ,如果 ,其中 是行驶时间的总和,则认为路线是可行的。
编写一个程序,根据 Flatland 铁路网络的描述和各个路线方案,确定每个方案是否存在可行的高速电车路线。
Input Format
第一行包含一个整数 ,表示测试数据的组数。
接下来的若干行描述每组测试数据。
每组测试数据的第一行包含四个整数 ,分别表示站点数量、线路数量、要考虑的路线方案数量和允许的时间偏差参数。
接下来的 行描述每条线路,每行包含三个整数 ,分别表示起始站点、终点站点和行驶时间。
接下来的 行描述每个路线方案,每行包含两个整数 和 ,分别表示目标站点和预计行驶时间。
Output Format
对于每个测试用例,输出一行长度为 的字符串 ,其中第 个字符 等于 表示存在可行的高速电车路线,行驶时间在区间 内;否则, 等于 表示不存在可行的高速电车路线。
2
3 3 5 20
1 2 20
2 3 1
1 3 10
2 19
2 20
3 20
3 21
3 9
7 10 5 5
1 2 15
1 3 10
2 4 21
3 4 30
2 5 14
3 5 31
4 6 3
5 6 14
1 7 39
5 7 13
7 42
7 43
7 44
5 39
6 44
11110
10111
1
4 6 5 2
1 2 1
2 3 1
3 4 1
1 2 70
2 3 120
3 4 4
4 90
4 2
4 10
4 37
2 34
11010
Hint
样例 解释:
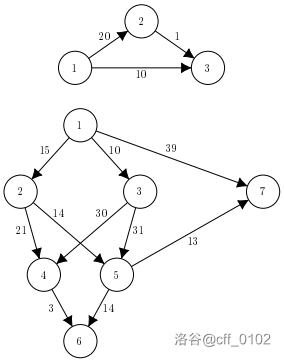
样例 解释:
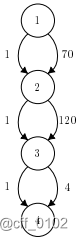
第一个查询的路线时间为 ,符合预期。
第二个查询的路线时间为 ,符合预期。
第四个查询的路线时间为 ,符合预期。
对于第三个和第五个查询,没有可行的路线符合预期。
数据范围:
对于 的数据,$1\le t\le1000,1\le v_i<u_i\le n\le500000,1\le m\le500000,1\le q\le500000,2\le p\le20,1\le d_i\le10^{11},2\le f_i\le n,1\le r_i\le10^{17}$。
各个 Subtask 分值及特殊性质:
| Subtask | 分值 | 其它特殊性质 | |||
|---|---|---|---|---|---|
| ,且对于每个 ,恰有两条从 出发到 的线路 | |||||
| 对于每个 ,恰有两条从 出发到 的线路 | |||||
| 所有 值相等 | |||||

 京公网安备 11011102002149号
京公网安备 11011102002149号