#P11053. [IOI 2024] 马赛克上色
[IOI 2024] 马赛克上色
Description
Salma 想给墙上的粘土马赛克上色。该马赛克由 片正方形瓷砖组成,共有 片瓷砖;每片瓷砖的尺寸为 ,都还没有上色。马赛克从上到下每行瓷砖的行编号从 到 ,从左到右每列瓷砖的列编号从 到 。位于第 行第 列(,)的瓷砖记为 。每片瓷砖要么涂成白色(记为 ),要么涂成黑色(记为 )。
为了给马赛克上色,Salma 首先选取两个长度为 的数组 和 ,每个数组都由 和 组成,并且 。她按照数组 对最上面的行(第 行)的瓷砖进行上色,使得瓷砖 的颜色为 ()。她按照数组 对最左边的列(第 列)的瓷砖进行上色,使得瓷砖 的颜色为 ()。
然后她重复以下步骤直至所有瓷砖都上色完成:
- 她找到任意一片没有上色的瓷砖 ,其上方相邻的瓷砖 和左边相邻的瓷砖 都已经上色。
- 然后,如果这两片相邻的瓷砖都是白色,她会把瓷砖 涂成黑色;否则,涂成白色。
可以证明,瓷砖最终的颜色不依赖于 Salma 的上色顺序。
Yasmin 对马赛克瓷砖的颜色非常好奇。她向 Salma 提出 个问题,从 到 编号。在问题 ()中,Yasmin 通过以下信息指定马赛克中的一个长方形:
- 最上面的行 和最下面的行 ();
- 最左边的列 和最右边的列 ()。
问题的答案是该长方形中黑色瓷砖的数量。具体来说,Salma 应当找出有多少片瓷砖 满足 ,,且颜色为黑色。
请编写程序回答 Yasmin 的问题。
实现细节
你要实现以下函数。
std::vector<long long> mosaic(
std::vector<int> X, std::vector<int> Y,
std::vector<int> T, std::vector<int> B,
std::vector<int> L, std::vector<int> R)
- ,:长度为 的数组,分别描述最上方行和最左边列的瓷砖的颜色。
- ,,,:长度为 的数组,分别描述 Yasmin 所提出的问题。
- 该函数应返回一个长度为 的数组 ,使得 给出问题 ()的答案。
- 对每个测试用例,该函数恰好被调用一次。
Input Format
评测程序示例读取如下格式的输入:
N
X[0] X[1] ... X[N-1]
Y[0] Y[1] ... Y[N-1]
Q
T[0] B[0] L[0] R[0]
T[1] B[1] L[1] R[1]
...
T[Q-1] B[Q-1] L[Q-1] R[Q-1]
Output Format
评测程序示例按照如下格式打印你的答案:
C[0]
C[1]
...
C[S-1]
其中 是 mosaic 所返回的数组 的长度。
4
1 0 1 0
1 1 0 1
2
0 3 0 3
2 3 0 2
7
3
Hint
考虑以下函数调用。
mosaic([1, 0, 1, 0], [1, 1, 0, 1], [0, 2], [3, 3], [0, 0], [3, 2])
该例子如下图所示。左边的图展示了马赛克中瓷砖的颜色,中间和右边的图分别展示了 Yasmin 的第一个问题和第二个问题中的长方形。
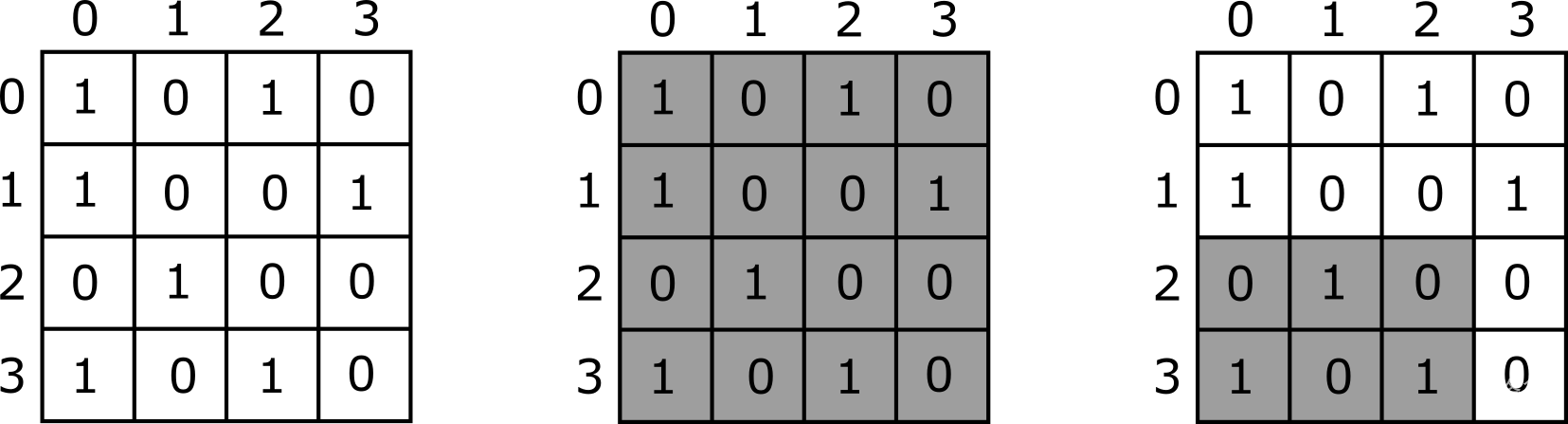
这两个问题的答案(即阴影长方形中 1 的个数)分别是 7 和 3。因此,函数应该返回 。
约束条件
- 对所有满足 的 ,都有 ,且
- 对所有满足 的 ,都有 ,且
| 子任务 | 分数 | 额外的约束条件 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | 对所有满足 的 ,都有 | |
| 4 | ||
| 5 | 对所有满足 的 ,都有 | |
| 6 | 对所有满足 的 ,都有 ,且 | |
| 7 | 对所有满足 的 ,都有 | |
| 8 | 没有额外的约束条件。 |

 京公网安备 11011102002149号
京公网安备 11011102002149号