题目背景

提交时请不要引用 tree.h。

请不要使用 C++14 (GCC 9) 提交。

题目描述

有一棵包括 $N$ 个结点的树，结点从 $0$ 到 $N-1$ 编号。结点 $0$ 是树的根。除根以外的每个结点都有唯一的父结点。对所有满足 $1 \leq i < N$ 的 $i$，结点 $i$ 的父结点为 $P[i]$，这里有 $P[i] < i$。我们约定 $P[0] = -1$。

对所有结点 $i$（$0 \leq i < N$），$i$ 的子树是如下结点组成的集合：

• $i$，以及
• 所有父结点为 $i$ 的结点，以及
• 所有父结点的父结点为 $i$ 的结点，以及
• 所有父结点的父结点的父结点为 $i$ 的结点，以及
• 以此类推。

下图给出了一个包含 $N = 6$ 个结点的树的例子。每个箭头都从某个结点连向它的父结点（根结点除外，因为它没有父结点）。结点 $2$ 的子树包括结点 $2, 3, 4$ 和 $5$。结点 $0$ 的子树包括树中的全部 $6$ 个结点，而结点 $4$ 的子树仅包括结点 $4$ 自己。

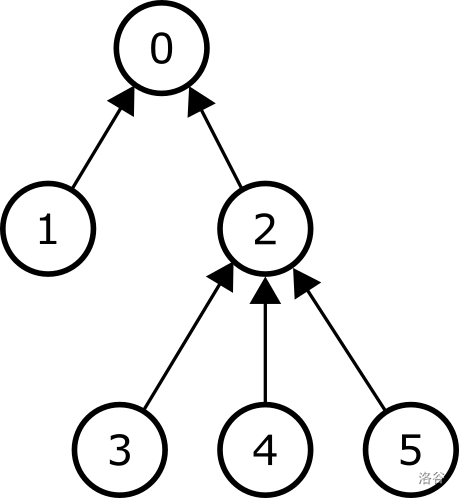
每个结点都被赋以非负整数的权重。我们将结点 $i$（$0 \leq i < N$）的权重记为 $W[i]$。

你的任务是写一个程序来回答 $Q$ 个询问，其中每个询问都用一对正整数 $(L, R)$ 来表示。对于询问的回答，应按照如下要求进行计算。

对树中的每个结点，都指派一个整数，称为系数。这样的指派结果被描述成一个序列 $C[0], \ldots, C[N-1]$，这里 $C[i]$（$0 \leq i < N$）是指派给结点 $i$ 的系数。我们称该序列为一个系数序列。注意，系数序列中的元素可以取负值、$0$ 或正值。

对某个询问 $(L, R)$，一个系数序列被称为是有效的，如果对于每个结点 $i$（$0 \leq i < N$）都有如下条件成立：结点 $i$ 的子树中的系数之和不小于 $L$ 且不大于 $R$。

对于一个给定的系数序列 $C[0], \ldots, C[N-1]$，结点 $i$ 的代价为 $|C[i]| \cdot W[i]$，这里 $|C[i]|$ 表示 $C[i]$ 的绝对值。最后，总体代价为所有结点的代价之和。你的任务是，对于每个询问，计算出可以由某个有效系数序列达到的最小总体代价。

可以证明，对于任意询问，都至少存在一个有效的系数序列。

实现细节

你需要实现如下两个函数：

void init(std::vector<int> P, std::vector<int> W)

• $P$，$W$：两个长度为 $N$ 的整数数组，记录了结点的父结点和权重。
• 对于每个测试样例，在评测程序与你的程序开始交互时，该函数将被恰好调用一次。

long long query(int L, int R)

• $L$，$R$：两个整数，描述一次询问。
• 对于每个测试样例，在 init 被调用后，该函数将被调用 $Q$ 次。
• 该函数应该返回对给定询问的答案。

输入格式

评测程序示例读取如下格式的输入：

N
P[1]  P[2] ...  P[N-1]
W[0]  W[1] ...  W[N-2] W[N-1]
Q
L[0]  R[0]
L[1]  R[1]
...
L[Q-1]  R[Q-1]

这里的 $L[j]$ 和 $R[j]$（$0 \leq j < Q$），是对 query 的第 $j$ 次调用的输入参数。注意，输入数据中的第二行中仅包括 $N-1$ 个整数，因为评测程序示例并不读取 $P[0]$ 的值。

输出格式

评测程序示例按照如下格式打印你的答案：

A[0]
A[1]
...
A[Q-1]

这里的 $A[j]$（$0 \leq j < Q$），是第 $j$ 次调用 query 时返回的值。

3
0 0
1 1 1
2
1 1
1 2

3
2

提示

考虑如下调用：

init([-1, 0, 0], [1, 1, 1])

这棵树包含 $3$ 个结点：根结点以及它的 $2$ 个子结点。所有结点的权重均为 $1$。

query(1, 1)

本次询问有 $L = R = 1$，这意味着每个子树中的系数之和都必须等于 $1$。考虑系数序列 $[-1, 1, 1]$。这棵树以及相应的系数（在阴影矩形中）图示如下。

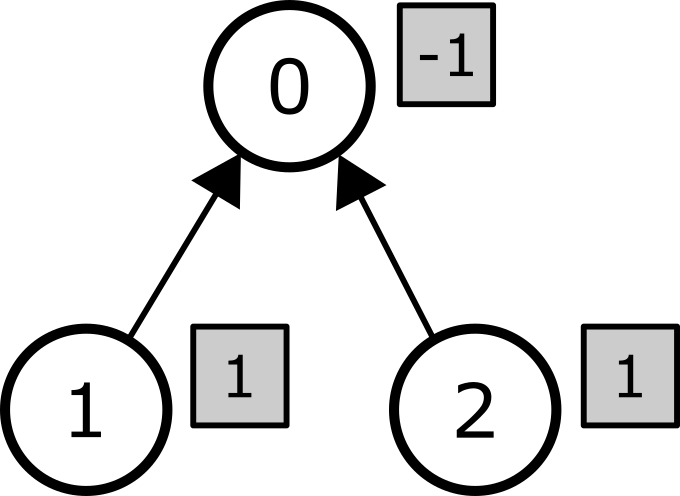
对每个结点 $i$（$0 \leq i < 3$），$i$ 的子树中全部结点的系数之和均为 $1$。因此，系数序列是有效的。总体代价的计算如下：

因此总体代价为 $3$。这是唯一的有效系数序列，因此调用应该返回 $3$。

query(1, 2)

对于该询问的最小总体代价为 $2$，可以在系数序列为 $[0, 1, 1]$ 时达到。

约束条件

• $1 \leq N \leq 200\,000$
• $1 \leq Q \leq 100\,000$
• $P[0] = -1$
• 对所有满足 $1 \leq i < N$ 的 $i$，都有 $0 \leq P[i] < i$
• 对所有满足 $0 \leq i < N$ 的 $i$，都有 $0 \leq W[i] \leq 1\,000\,000$
• 在每次询问中，都有 $1 \leq L \leq R \leq 1\,000\,000$