#P10770. 「CROI · R2」夏风与树
「CROI · R2」夏风与树
Description
Alice and Bob are planting trees while playing a game.
Alice owns nodes , and Bob owns nodes . The weights of these nodes form a permutation , where is the weight of node .
First, they agree that node is the root of the tree.
Then, Alice decides the parent for nodes , where the parent of node must be chosen from .
Next, Bob decides the parent for nodes , where the parent of node can be chosen from . Node is not part of their tree, meaning Bob's nodes do not need to be connected to this tree.
Finally, Alice will perform a depth-first search starting from node . During this process, she maintains a sequence: whenever she encounters an unvisited node, she appends its weight to the end of the sequence.
Alice wants the lexicographical order of the final sequence to be as small as possible, while Bob wants it to be as large as possible. Both will adopt optimal strategies. Now Bob asks you to determine what the final sequence will be.
Definitions related to lexicographical order:
- For a sequence of length , if , we define .
- For two sequences and , we say is lexicographically smaller than if there exists an such that for all , , and .
Input Format
In some test cases of this problem, Bob will provide you with the parents of nodes determined by Alice in the first step.
The first line contains an integer , representing the subtask number. Notably, the sample input has subtask number .
The second line contains a positive integer .
The third line contains positive integers, representing the permutation .
The fourth line contains integers. If the subtask has Special Property A, these integers represent the parents of nodes . Otherwise, all integers are .
Output Format
A single line representing the final sequence.
0
5
10 5 1 8 4 3 7 6 2 9
1 1 1 3
10 1 4 9 7 6 5 8 3 2
0
4
7 2 4 1 5 6 3 8
0 0 0
7 1 8 2 4 6 5 3
0
4
2 7 6 4 5 8 1 3
0 0 0
2 4 8 6 7 5 3
Hint
In Sample #1, a possible final tree is shown (numbers are node IDs, values in parentheses are weights):
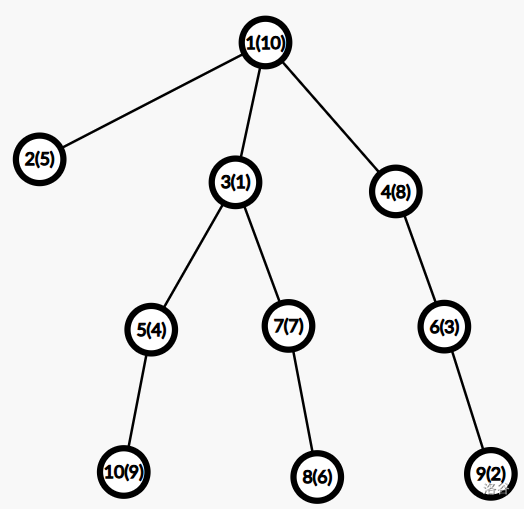
Data Range
| Subtask | Points | Special Properties | |
|---|---|---|---|
| None | |||
| B | |||
| A | |||
| None | |||
Special Property A: The input provides the parents of nodes under one of Alice's optimal strategies.
Special Property B: form a permutation of .
For of the data: , and the sequence is guaranteed to be a permutation of .

 京公网安备 11011102002149号
京公网安备 11011102002149号