#P10763. [BalticOI 2024] Tiles
[BalticOI 2024] Tiles
Description
有一个存在 个顶点的大教堂,顶点坐标依次为 ,对于每个 ,存在一条 与 之间的边,此外,还存在一条 到 的边。
大教堂每条边都与 轴或 轴平行。此外,大教堂是一个简单多边形,即:
- 每个顶点恰好由两条边相交
- 任何一对边只能在顶点处相交
你有无数块 的瓷砖,你希望用这些瓷砖覆盖大教堂的大部分区域,具体来说,你想选择一条垂直线,并覆盖该线左侧的大教堂部分。对于任何整数 ,设 为包含 坐标等于 的点的垂直线。对 左侧大教堂部分的覆盖,是指在平面上放置一定数量的瓷砖,使得:
- 多边形内部且 坐标小于 的每个点都被某块瓷砖覆盖
- 多边形外部或 坐标大于 的点都不被任何瓷砖覆盖
- 瓷砖的内部不重叠
大教堂中任何顶点的最小 坐标为 。我们设 为大教堂中任何顶点的最大 坐标。
请你求出最大的满足条件的 ,根据定义,一定存在答案为 。
Input Format
第一行两个整数 。
接下来 行,每行两个整数 。这些顶点按照顺时针或逆时针顺序给出。
Output Format
输出一个答案 。
14 6
0 1
0 3
2 3
2 4
0 4
0 6
3 6
3 7
4 7
6 7
6 5
3 5
3 2
3 1
2
4 3
0 0
0 3
3 3
3 0
0
18 9
0 2
2 2
2 1
4 1
4 0
9 0
9 2
4 2
4 4
7 4
7 3
9 3
9 6
4 6
4 5
2 5
2 4
0 4
6
Hint
| 子任务编号 | 特殊性质 | 分值 |
|---|---|---|
| ,对于 , | ||
| 且 | ||
| 都为偶数 | ||
| 都为偶数 | ||
| 无特殊性质 |
对于所有数据,,,,。
对于样例一,下面是对于 的覆盖。
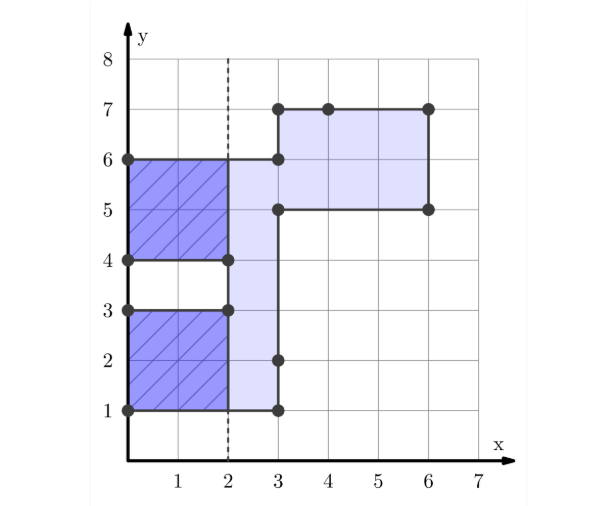
可以发现这是最大的情况了。
对于样例二,没有正值 ,使得 左侧的教堂部分可以用瓷砖覆盖。
对于样例三,图示如下。
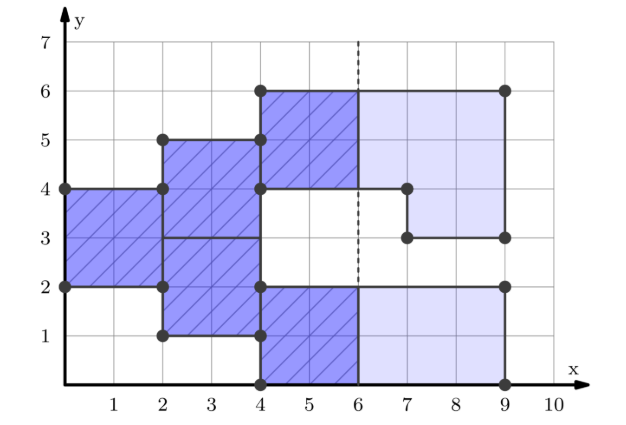

 京公网安备 11011102002149号
京公网安备 11011102002149号