#P10698. [SNCPC2024] 最大流
[SNCPC2024] 最大流
Description
给定一个 个点 条边的有向无环图,图中每条边的容量为 。对点 以外的每个点 ,设从点 到点 的最大流为 ,试求出 。
在边容量为 的图上,一个从点 到点 的流即为一条从点 到点 的路径。如果从点 到点 最多能同时有 个不交的流(即没有一条边同时属于两个流),则我们认为点 到点 的最大流是 。
Input Format
输入第一行为三个整数 ($2 \leq n \leq 10^5, 1 \leq m \leq 2 \times 10^5, 1 \leq k \leq 50$),由空格隔开,为图的点数,边数和参数。
接下来 行,每行两个整数 (),由空格隔开,描述一条有向边。
图中保证没有自环,但是可能存在重边,保证给出的是一个有向无环图。
Output Format
输出仅一行 个整数,由空格隔开。对于第 个整数,如果从结点 到结点 的最大流不超过 ,则为最大流的值,否则为 。
7 12 3
1 2
1 3
3 2
3 4
2 4
1 5
5 6
3 6
1 7
5 7
6 7
4 7
2 1 2 1 2 3
5 8 50
1 2
1 2
1 2
3 2
2 4
2 4
2 4
2 4
3 0 3 0
Hint
第一个样例所述图如下:
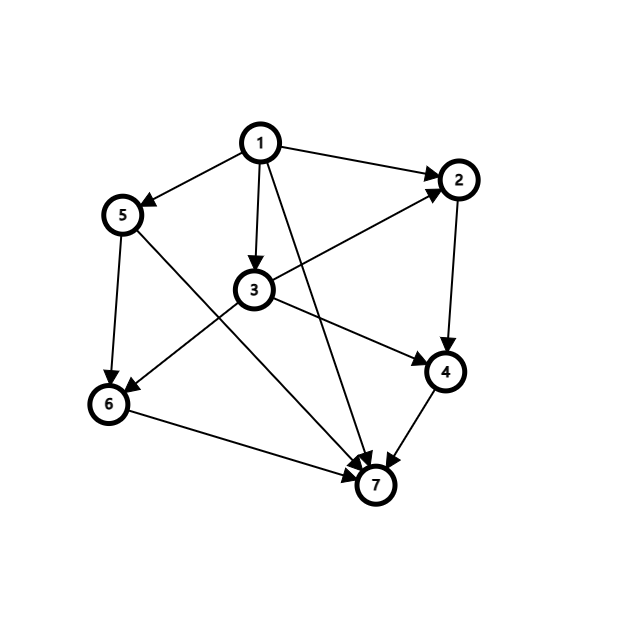
我们可以找到 条从点 到点 的不相交路径:
我们无法找到更多条从点 到点 的不相交路径:
所以点 到点 的最大流为 ,但是因为 ,所以答案的第六个整数为 。

 京公网安备 11011102002149号
京公网安备 11011102002149号