题目背景

请勿使用 C++14(GCC9) 提交

杭州市的中心广场有一棵著名的古树。这棵古树可以看作一棵 $N$ 个节点的有根树，节点编号从 $0$ 到 $N - 1$，其中 $0$ 号节点是根节点。

称没有孩子的节点为叶子节点。古树每次落叶时，会选择一个当前的叶子节点删去。每一天中，古树可能会多次落叶。

有 $M$ 位志愿者（编号从 $0$ 到 $M - 1$）负责看护古树。每一位志愿者将各自按照如下方式独立记录今年的落叶的情况：

每一天，收集所有新的落叶的编号（即当天删除的节点的编号），然后将它们按任意顺序写在先前的落叶编号之后。

例如：第一天，叶子 $3$ 和 $4$ 落下，于是他们写下 $3, 4$ 或 $4, 3$。第二天，叶子 $1$ 和 $2$ 落下，于是他们继续写下 $1, 2$ 或 $2, 1$。最终的记录可能为 $(3, 4, 1, 2)$，$(4, 3, 1, 2)$，$(3, 4, 2, 1)$ 或 $(4, 3, 2, 1)$ 中的任意一个。

这个过程持续了 $K$ 天，每天都有新的叶子掉落，直到只剩根节点为止。

你在旅途过程中经过了杭州。此刻已是寒冬，仰望古树光秃秃的枝干，你不禁想起落叶纷飞的美丽景象。

你很想知道今年有几天能看见落叶，但你只能找到 $M$ 位志愿者的记录。尝试根据这些记录推断出 $K$ 可能的最大值。

题目描述

你无需在程序开头引入库 september.h。

你只需要实现以下函数：

int solve(int N, int M, std::vector<int> F,
            std::vector<std::vector<int>> S);

• $N$：古树的节点数量。
• $M$：志愿者的数量。
• $F$：一个长度为 $N$ 的数组。对于 $1 \le i \le N - 1$，$F[i]$ 表示节点 $i$ 的父亲节点的编号。$F[0]$ 始终为 $-1$。
• $S$：一个长度为 $M$ 的数组。$S$ 中的每个元素是一个长度为 $N - 1$ 的数组。$S[i][j]$ 表示志愿者 $i$ 记录的第 $j$ 个节点编号（从 $0$ 开始）。
• 该函数必须返回一个整数，表示根据如上规则的 $K$ 可能的最大值（即，最大可能的落叶天数）。
• 对于每个测试点，交互库可能调用该函数多于一次。每次调用都应该作为新的情况分别处理。

注意：由于函数调用可能会发生多次，选手需要注意之前调用的残余数据对于后续调用的影响，尤其是全局变量的状态。

输入格式

评测程序示例读取如下格式的输入：

• 第 1 行：$T$

对于接下来 $T$ 组数据中的每一组：

• 第 $1$ 行：$N\ M$
• 第 $2$ 行：$F[1]\ F[2]\ \ldots\ F[N - 1]$
• 第 $3 + i\ (0 \le i \le M - 1)$ 行：$S[i][0]\ S[i][1]\ S[i][2]\ \ldots\ S[i][N - 2]$

输出格式

评测程序示例按照如下格式打印你的答案：

对于每组测试数据：

• 第 1 行：函数 solve 的返回值

1
3 1
0 0
1 2

2

1
5 2
0 0 1 1 
1 2 3 4
4 1 2 3

1

提示

样例解释

对于样例一，考虑如下调用：

solve(3, 1, {-1, 0, 0}, {{1, 2}});

对应的树如下图所示：

叶子 $1$ 和 $2$ 可能在同一天落下，或者叶子 $1$ 在第一天先落下，然后叶子 $2$ 在第二天落下。落叶天数不超过 $2$。

因此，程序应当返回 $2$。

对于样例二，考虑如下调用：

solve(5, 2, {-1, 0, 0, 1, 1}, {{1, 2, 3, 4}, {4, 1, 2, 3}});

对应的树如下图所示：

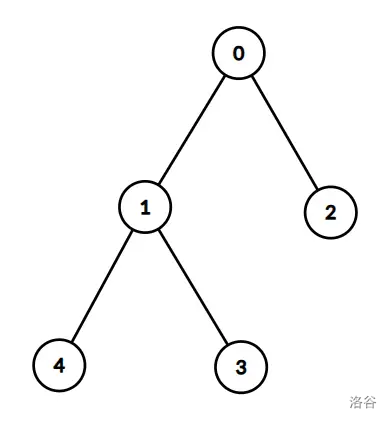
假设至少有 $2$ 天落叶，根据志愿者的记录，叶子 $4$ 将在不同的日子（第一天和最后一天）落下，这是矛盾的。

因此，程序应当返回 $1$。

数据范围

• $2 \le N \le 10^5$
• $1 \le M \le 5$
• $\sum NM \le 8 \times 10^5$
• $F[0] = -1$ 且对于 $1 \le i \le N - 1$, $0 \le F[i] \le i - 1$
• 对于 $1 \le i \le M - 1$, 数组 $S[i]$ 是一个 $1, 2, \ldots , N - 1$ 的排列
• 保证 $F$ 描述的是一棵以节点 $0$ 为根的有根树

详细子任务附加限制及分值如下表所示。