Description

“独眼小宝”是托克最喜欢的玩具，作为璃月最好的玩具销售员，达达利亚共招募了 $N$ 位经销商负责分销“独眼小宝”，$N$ 位经销商依次编号为 $1,2,\cdots,N$。

$N$ 位经销商中共形成了 $M$ 对交易关系，依次编号为 $1,2,\cdots,M$，第 $i$ 对交易关系联系起经销商 $u_i,v_i$。对于第 $i$ 对交易关系，当一方获知“独眼小宝”的生产情报时，将有 $\dfrac{p_i}{q_i}$ 的概率告知另一方。形式化地，经销商和他们之间的交易关系构成了一张无向图，数据保证这张无向图是连通的、无自环的和无重边的。

一些经销商 $a_1,a_2,\cdots,a_k(k>2)$ 构成商业集团，当且仅当存在 $k$ 组不同的交易关系，使得第 $w$ 组关系联系起经销商 $a_w,a_{w \bmod k+1}$。形式化地，一个商业集团对应 $k$ 名经销商和他们的交易关系图中的一个简单环。一名经销商最多属于一个商业集团。

现在，达达利亚希望对这些经销商进行测试，他共进行了 $Q$ 次独立的测试。对于第 $i$ 次测试，达达利亚将“独眼小宝”的生产情报告知了经销商 $S_i$，请问期望条件下，共有多少名经销商会得知该情报？

可以证明，期望一定可以被表示为 $\dfrac{p}{q}$ 的形式，你需要输出 $p\cdot q^{-1}\pmod {998\ 244\ 353}$ 的值。

Input Format

输入共 $M+Q+1$ 行。

输入的第一行为三个正整数 $N,M,Q$，分别表示经销商数量、交易关系数量和测试次数。

接下来 $M$ 行，每行四个正整数 $u_i,v_i,p_i,q_i$，表示第 $i$ 条交易关系联系的经销商与告知概率。

接下来 $Q$ 行，每行一个整数 $S_i$，表示第 $i$ 次测试所告知的经销商。

Output Format

输出 $Q$ 行。对于每组询问，输出一行一个整数，表示期望对 $998\ 244\ 353$ 取模的结果。

4 4 1
1 2 1 2
3 2 1 3
3 4 1 5
2 4 1 2
1

565671802

9 9 5
9 3 3 5
9 1 1 2
9 2 1 1
4 7 4 5
2 4 2 3
6 8 1 4
5 6 1 3
3 5 2 5
8 3 3 5
1
3
4
7
5

35936800
46584741
380663851
584039500
757135070

见选手目录下的 tartaglia/tartaglia3.in 与 tartaglia/tartaglia3.ans。

该样例满足测试点 1 ∼ 2 的限制。

见选手目录下的 tartaglia/tartaglia4.in 与 tartaglia/tartaglia4.ans。

该样例满足测试点 10 ∼ 13 的限制。

见选手目录下的 tartaglia/tartaglia5.in 与 tartaglia/tartaglia5.ans。

该样例满足测试点 14 ∼ 19 的限制。

见选手目录下的 tartaglia/tartaglia6.in 与 tartaglia/tartaglia6.ans。

Hint

样例解释 1

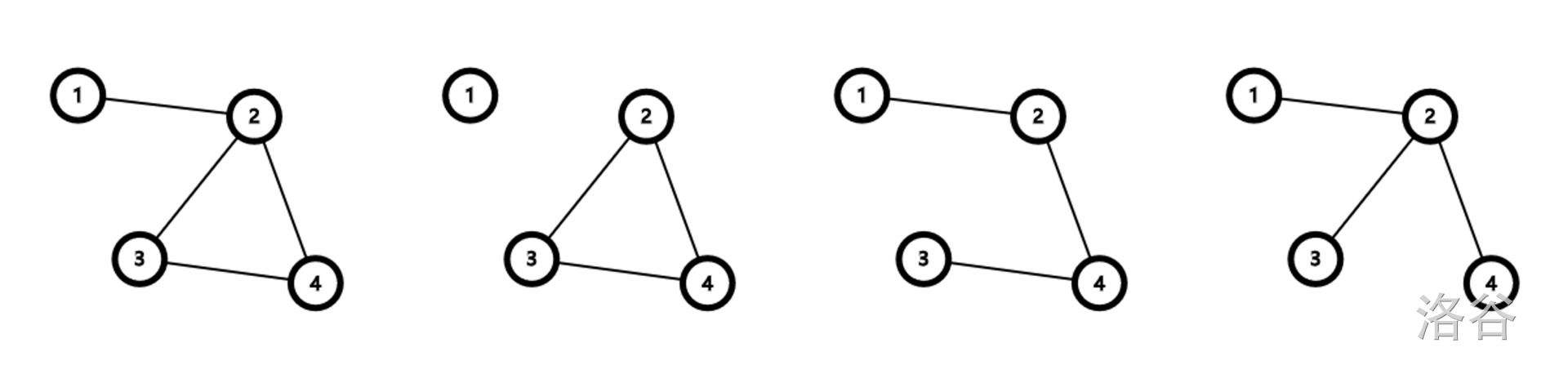
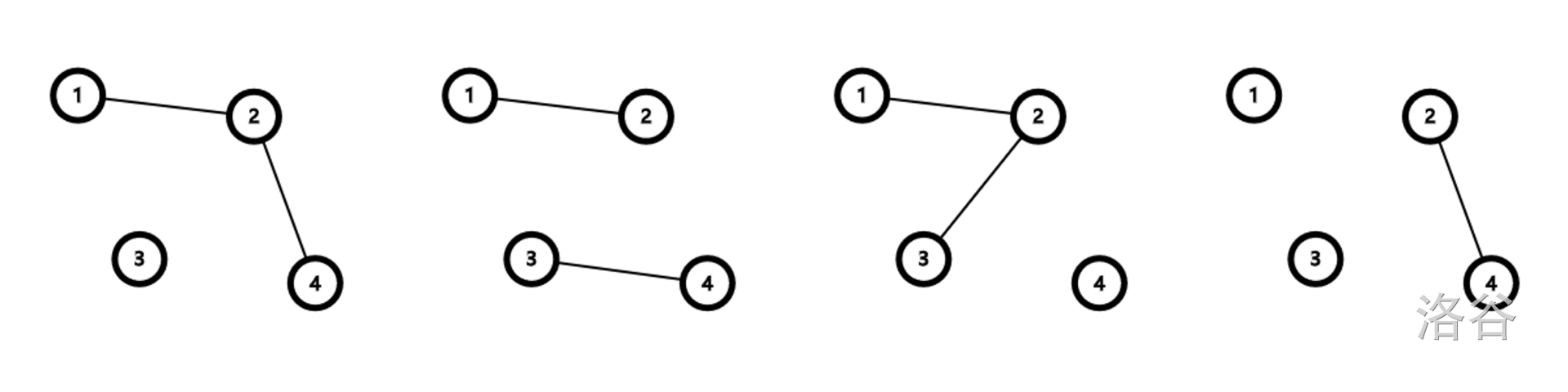
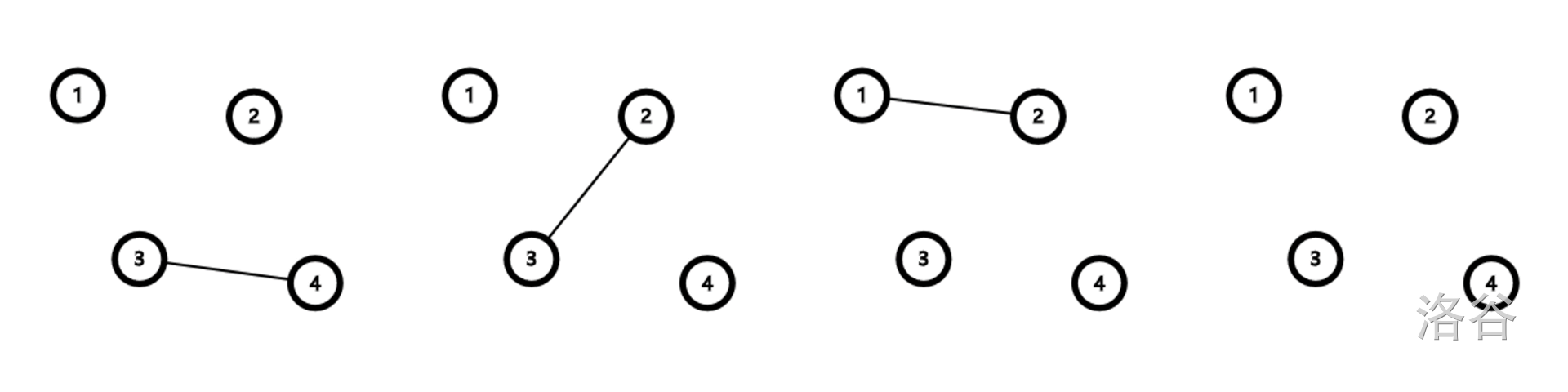
上图展现了所有的 $16$ 种可能的图连通情况，从上至下，从左至右，依次编号为 $1\sim 16$。对于节点 $1$ 的询问，我们依次计算 $16$ 种情况中节点 $1$ 能到达的节点数和该情况对应的概率：

求和，得到 $E=\sum E_i=\frac{59}{30}\equiv 565\ 671\ 802\pmod{998\ 244\ 353}$。

子任务

对于所有测试数据，保证 $1 \leq N,M,Q \leq 3 \times 10^5$，$1 \le u_i,v_i \le N$，$u_i\neq v_i$，$1 \le p_i,q_i < 998\ 244 \ 353$，$1 \le S_i \le N$。

特殊性质 A：不存在集团。

特殊性质 B：有且只有一个集团。

提示

在本题中，你可能需要使用较大的栈空间。在最终测试时，程序可使用的栈空间内存限制与题目内存限制一致。

若你使用 Linux 系统，可使用命令 ulimit -s unlimited 解除系统栈空间限制。若你使用 Windows 系统，可在编译命令后添加 -Wl,--stack=1024000000，以将系统栈空间限制修改为约 1024MiB。