题目描述

在一个平行宇宙里，每个人都在 CCO 上得了满分。因此，Troy 需要根据抽奖来选出获胜者。每个参赛者将选择一些数字来创建一张彩票。一张彩票是一个大小为 $N$ 的数组，从 $1$ 到 $N$ 编号，其中每个元素是从 $0$ 到 $K$ 的一个数字。

中奖彩票是由将 $K$ 个球（编号为 $1$ 到 $K$）按随机顺序投入一个有根二叉树来确定的。这棵树有 $N$ 个节点（编号为 $1$ 到 $N$），并以节点 $1$ 为根。

每个球都有一个指定的投放节点，它将在那里投放。当一个球投放在一个空节点或进入一个空节点时，会发生以下三种情况之一：

1. 如果当前节点的所有子节点都被球占据（或者如果一个节点没有子节点），那么当前球就会停留在当前节点。也就是说，它会留在那里，不再移动。
2. 如果当前节点只有一个空的子节点，那么当前球将移动到这个子节点。
3. 如果当前节点有两个空的子节点，而且如果当前球刚刚被投放，它可以向左或向右移动。否则，它将继续沿着它之前的移动方向移动。

如果 $K$ 个球不能全部被投放，那么就没有确定的中奖彩票。这种情况发生在一个球被投放时，它的投放节点被另一个球占据了。

如果所有 $K$ 个球都被投放了，那么球的停留位置就决定了中奖彩票。中奖彩票的第 $i$ 个元素是停留在节点 $i$ 的球的编号，或者如果没有球停留在节点 $i$，就是 $0$。

Troy 想知道可能的中奖彩票的数量。因为答案可能很大，你只需要求数量对 $10^9+7$ 取模的结果。

输入格式

第一行包含两个用空格分隔的整数 $N$ 和 $K$，表示二叉树中的节点数和球的数目。

第二行包含 $K$ 个用空格分隔的整数，其中第 $i$ 个整数表示编号为 $i$ 的球的指定投放节点。

最后 $N$ 行，每行包含两个用空格分隔的整数。第 $i$ 行包含 $L_{i}$ 和 $R_{i}$，表示第 $i$ 个节点的左子节点和右子节点，其中 $0$ 表示子节点不存在。

输出格式

输出中奖彩票的数量模 $10^{9}+7$。

5 2
1 3
2 3
0 0
4 5
0 0
0 0

4

4 3
1 2 4
0 2
0 3
0 4
0 0

2

提示

样例 1 解释

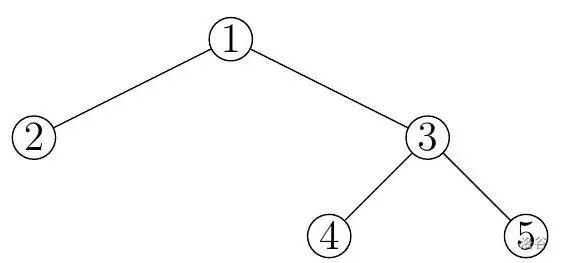
考虑当球 $1$ 先被投放时。如果球 $1$ 向左移动，那么它将停留在节点 $2$。之后，球 $2$ 被投放，可以停留在节点 $4$ 或 $5$。如果球 $1$ 向右移动，它将停留在节点 $5$。然后，球 $2$ 将停留在节点 $4$。

考虑当球 $2$ 先被投放时。球 $2$ 可以向左或向右移动，分别停留在节点 $4$ 或 $5$。然后如果球 $1$ 在被投放后向左移动，它将停留在节点 $2$。然而，如果球 $1$ 向右移动，它将停留在节点 $4$ 或 $5$，取决于球 $2$ 没有占据的位置。

可能的中奖彩票是 $[0,1,0,2,0],[0,1,0,0,2],[0,0,0,1,2]$ 和 $[0,0,0,2,1]$。

样例 2 解释

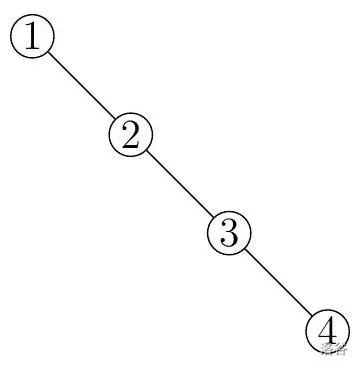
这个样例满足第二个子任务的条件。

球 $3$ 必须先被投放，因为如果球 $1$ 或球 $2$ 在球 $3$ 之前被投放，它会停留在节点 $4$，这不会让球 $3$ 被投放。

因此，我们可以先投放球 $3$，然后投放球 $2$，最后投放球 $1$，或者我们可以先投放球 $3$，然后投放球 $1$，最后投放球 $2$。对应的中奖彩票是 $[0,1,2,3]$ 和 $[0,2,1,3]$。

数据范围

对于所有的数据，有 $1\leq N,K \leq 4000$。

子任务编号	分值	$N$ 的范围	$K$ 的范围	额外的约束
$1$	$12$	$1 \leq N \leq 12$	$1 \leq K \leq 6$	无
$2$	$16$	$1 \leq N \leq 4000$	$1 \leq K \leq 4000$	所有节点都没有左子节点
$3$	$36$			$N$ 个投放节点是不同的
$4$				无